
【题目】将函数![]() 的图象,向右平移
的图象,向右平移![]() 个单位长度,再把纵坐标伸长到原来的2倍,得到函数
个单位长度,再把纵坐标伸长到原来的2倍,得到函数![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 函数![]() 的最小正周期为
的最小正周期为![]() B. 函数
B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() D.
D. ![]() 是函数
是函数![]() 的一条对称轴
的一条对称轴
【答案】C
【解析】
利用函数y=Asin(ωx+φ)的图象变换规律,求得f(x)的解析式,再利用正弦函数的图象和性质,判断各个选项是否正确.
将函数g(x)=2cos2(x+![]() )﹣1=cos(2x+
)﹣1=cos(2x+![]() )的图象向右平移
)的图象向右平移![]() 个单位长度,
个单位长度,
可得y=cos(2x﹣![]() +
+![]() )=cos(2x﹣
)=cos(2x﹣![]() )的图象;
)的图象;
再把纵坐标伸长到原来的2倍,得到函数f(x)=2cos(2x﹣![]() )的图象.
)的图象.
显然,f(x)的最小正周期为![]() =π,故A错误.
=π,故A错误.
在区间[![]() ]上,2x﹣
]上,2x﹣![]() ∈[π,
∈[π,![]() ],函数g(x)没有单调性,故B错误.
],函数g(x)没有单调性,故B错误.
在区间[![]() ]上,2x﹣
]上,2x﹣![]() ∈[
∈[![]() ,
,![]() ],故当2x﹣
],故当2x﹣![]() =
=![]() 时,函数f(x)取得最小值为﹣
时,函数f(x)取得最小值为﹣![]() ,故C正确.
,故C正确.
当x=![]() 时,f(x)=2cos(2x﹣
时,f(x)=2cos(2x﹣![]() )=0,不是最值,故x=
)=0,不是最值,故x=![]() 不是函数f(x)的一条对称轴,故D错误,
不是函数f(x)的一条对称轴,故D错误,
故选:C.


科目:高中数学 来源: 题型:
【题目】约定乒乓球比赛无平局且实行![]() 局
局![]() 胜制,甲、乙二人进行乒乓球比赛,甲每局取胜的概率为
胜制,甲、乙二人进行乒乓球比赛,甲每局取胜的概率为![]() .
.
(1)试求甲赢得比赛的概率;
(2)当![]() 时,胜者获得奖金
时,胜者获得奖金![]() 元,在第一局比赛甲获胜后,因特殊原因要终止比赛.试问应当如何分配奖金最恰当?
元,在第一局比赛甲获胜后,因特殊原因要终止比赛.试问应当如何分配奖金最恰当?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题,按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
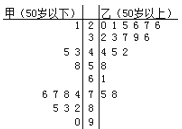
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() 的直线与抛物线交于
的直线与抛物线交于![]() 两点,且
两点,且![]() ,抛物线的准线
,抛物线的准线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 于点
于点![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() ,过
,过![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 两点,且
两点,且![]() ,点
,点![]() 为线段
为线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点,则点
轴的交点,则点![]() 的横坐标
的横坐标![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,离心率为
,离心率为![]() ,已知过
,已知过![]() 轴上一点
轴上一点![]() 作一条直线
作一条直线![]() :
:![]() ,交椭圆于
,交椭圆于![]() 两点,且
两点,且![]() 的周长最大值为8.
的周长最大值为8.
(1)求椭圆方程;
(2)以点![]() 为圆心,半径为
为圆心,半径为![]() 的圆的方程为
的圆的方程为![]() .过
.过![]() 的中点
的中点![]() 作圆的切线
作圆的切线![]() ,
,![]() 为切点,连接
为切点,连接![]() ,证明:当
,证明:当![]() 取最大值时,点
取最大值时,点![]() 在短轴上(不包括短轴端点及原点).
在短轴上(不包括短轴端点及原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
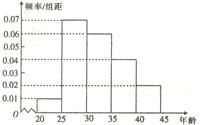
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com