
分析 利用两角和的正切将tan(α+β)=9tanβ转化,整理为关于tanβ的一元二次方程,利用题意,结合韦达定理即可求得答案.
解答 解:∵tan(α+β)=9tanβ,
∴$\frac{tanα+tanβ}{1-tanαtanβ}$=9tanβ,
∴9tanαtan2β-8tanβ+tanα=0,①
∴α,β∈(0,$\frac{π}{2}$),
∴方程①有两正根,tanα>0,
∴△=64-36tan2α≥0,
∴0<tanα≤$\frac{4}{3}$.
∴tanα的最大值是$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查两角和与差的正切函数,考查一元二次方程中韦达定理的应用,考查转化思想与方程思想,也可以先求得tanα,再利用基本不等式予以解决,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | B. | $({\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ | C. | $({-\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | D. | $({-\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,其短轴的下端点在抛物线x2=4y的准线上.
已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,其短轴的下端点在抛物线x2=4y的准线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
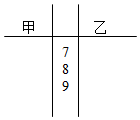 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):查看答案和解析>>
科目:高中数学 来源: 题型:选择题
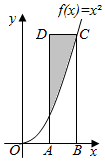 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.
如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com