Question

12．甲乙两组数学兴趣小组的同学举行了赛前模拟考试，成绩记录如下（单位：分）：
甲：79，81，82，78，95，93，84，88
乙：95，80，92，83，75，85，90，80
（1）画出甲、乙两位学生成绩的茎叶图，；
（2）计算甲、乙两组同学成绩的平均分和方差，并从统计学的角度分析，哪组同学在这次模拟考试中发挥比较稳定；
（3）在甲、乙两组同学中，若对成绩不低于90分得再随机地抽3名同学进行培训，求抽出的3人中既有甲组同学又有乙组同学的概率．
（参考公式：样本数据x₁，x₂，…，x_n的标准差：
s=$\sqrt{\frac{1}{n}[（{x}_{1}-\overline{x}）^{2}+（{x}_{2}-\overline{x}）^{2}+…+（{x}_{n}-\overline{x}）^{2}]}$，其中$\overline{x}$为样本平均数）

Answer 1

分析 （1）由甲乙两组的成绩纪录，能作出甲、乙两位学生成绩的茎叶图．
（2）分别求出甲组同学成绩的平均分、方差和乙组同学成绩的平均、方差，由甲和乙两组同学成绩平均分相等，乙组同学成绩的方差大于甲组同学成绩的方差，得甲组同学模拟考试中发挥比较稳定．
（3）在甲、乙两组同学中，成绩不低于90分的有5人，其中甲组2人，乙组3人，由此利用对立事件概率计算公式能求出抽出的3人中既有甲组同学又有乙组同学的概率．

解答 解：（1）由甲乙两组的成绩纪录，作出甲、乙两位学生成绩的茎叶图如下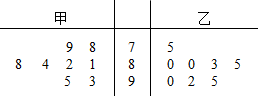

（2）甲组同学成绩的平均分$\overline{{x}_{甲}}$=$\frac{1}{8}$（79+81+82+78+95+93+84+88）=85，
甲组同学成绩的方差${{S}_{甲}}^{2}$=$\frac{1}{8}$[（79-85）²+]（81-85）²+（82-85）²+（78-85）²+（95-85）²+（93-85）²+（84-85）²+（88-85）²]=35.5．
乙组同学成绩的平均分$\overline{{x}_{乙}}$=$\frac{1}{8}$（95+80+92+83+75+85+90+80）=85，
乙组同学成绩的方差${{S}_{乙}}^{2}$=$\frac{1}{8}$[（95-85）²+]（80-85）²+（92-85）²+（83-85）²+（75-85）²+（85-85）²+（90-85）²+（80-85）²]=41．
∵甲和乙两组同学成绩的平均分相等，乙组同学成绩的方差大于甲组同学成绩的方差，
∴甲组同学模拟考试中发挥比较稳定．
（3）在甲、乙两组同学中，成绩不低于90分的有5人，其中甲组2人，乙组3人，
从中任取3人，基本事件总数n=${C}_{5}^{3}$=10，
抽出的3人中既有甲组同学又有乙组同学的概率：
p=1-$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=$\frac{9}{10}$．

点评 本题考查茎叶图的作法，考查平均分、方差的求法，考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．