

| A. | k<14 | B. | k<15 | C. | k<16 | D. | k<17 |
分析 根据程序框图,写出运行结果,根据程序输出的结果是S=-4,可得出判断框内应填入的条件.
解答 解:执行如图的程序框图,运行结果如下:
第1次循环S=log2$\frac{1}{2}$=-1,k=2;
第2次循环S=log2$\frac{1}{2}$+log2$\frac{2}{3}$=log2$\frac{1}{3}$,k=3;
第3次循环S=log2$\frac{1}{3}$+log2$\frac{3}{4}$=log2$\frac{1}{4}$=-2,k=4;
第4次循环S=log23$\frac{1}{4}$+log2$\frac{4}{5}$=log2$\frac{1}{5}$,k=5;
第5次循环S=log2$\frac{1}{5}$+log2$\frac{5}{6}$=log2$\frac{1}{6}$,k=6;
第6次循环S=log2$\frac{1}{6}$+log2$\frac{6}{7}$=log2$\frac{1}{7}$,k=7;
第7次循环S=log2$\frac{1}{7}$+log24$\frac{7}{8}$=log2$\frac{1}{8}$=-3,k=8;
…
第14次循环S=log2$\frac{1}{14}$+log2$\frac{14}{15}$=log2$\frac{1}{15}$,k=15;
第15次循环S=log2$\frac{1}{15}$+log2$\frac{15}{16}$=log2$\frac{1}{16}$=-4,•k=16;
如果输出S=-4,那么只能进行15次循环,故判断框内应填入的条件是k<16.
故选:C.
点评 本题考查程序框图,尤其考查循环结构,对循环体每次循环需要进行分析并找出内在规律,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组[1,3),第二组[3,5),第三组[5,7),第四组[7,9),第五组[9,11],绘制成如图所示的频率分布直方图.
某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组[1,3),第二组[3,5),第三组[5,7),第四组[7,9),第五组[9,11],绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
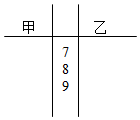 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com