
分析 由双曲线一条渐近线的斜率的取值范围求出3<m<5,由此能求出焦点在x轴上的椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1的离心率e的取值范围.
解答 解:∵双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{m}$=1的一条渐近线的斜率的取值范围为($\frac{\sqrt{3}}{2}$,$\frac{\sqrt{5}}{2}$),
∴$\frac{\sqrt{3}}{2}<\frac{\sqrt{m}}{2}<\frac{\sqrt{5}}{2}$,解得3<m<5,
∴焦点在x轴上的椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1中,
a=$\sqrt{5}$,$\sqrt{3}<b=\sqrt{m}<\sqrt{5}$,
∴e=$\frac{c}{a}=\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{5-m}}{\sqrt{5}}$∈(0,$\frac{\sqrt{10}}{5}$).
∴焦点在x轴上的椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1的离心率e的取值范围是(0,$\frac{\sqrt{10}}{5}$).
点评 本题考查椭圆的斜率的取值范围的求法,是中档题,解题时要认真审题,注意双曲线、椭圆的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=cos$\frac{πx}{3}$ | B. | $f(x)=sin\frac{πx}{3}$ | C. | f(x)=2cos2$\frac{πx}{6}$ | D. | f(x)=2cos2$\frac{πx}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
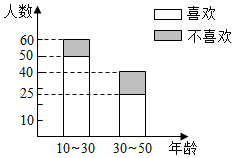 某电视台为调查市民对本台某节目的喜爱是否与年龄有关,随机抽取了100名市民,其中是否喜欢该节目的人数如图所示:
某电视台为调查市民对本台某节目的喜爱是否与年龄有关,随机抽取了100名市民,其中是否喜欢该节目的人数如图所示:| 喜欢 | 不喜欢 | 合计 | |
| 10岁至30岁 | a | b | 60 |
| 30岁至50岁 | c | d | 40 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com