
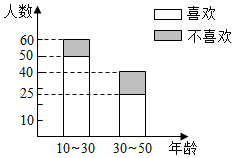
 ij����̨Ϊ��������Ա�̨ij��Ŀ��ϲ���Ƿ��������йأ������ȡ��100�����������Ƿ�ϲ���ý�Ŀ��������ͼ��ʾ��
ij����̨Ϊ��������Ա�̨ij��Ŀ��ϲ���Ƿ��������йأ������ȡ��100�����������Ƿ�ϲ���ý�Ŀ��������ͼ��ʾ��| ϲ�� | ��ϲ�� | �ϼ� | |
| 10����30�� | a | b | 60 |
| 30����50�� | c | d | 40 |
| �ϼ� | 75 | 25 | 100 |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ��1������a��b��c��d��ֵ����д���������ɣ�
��2������۲�ֵK2��ͨ���������ݵó����ʽ��ۣ�
��3�����÷ֲ����ԭ�������10�ꡫ30�ꡱ�롰30�ꡫ50�ꡱ���������������оٷ���������¼����������Ӧ�ĸ��ʼ��ɣ�
��� �⣺��1��a=50��b=10��c=25��d=15��������£�
| ϲ�� | ��ϲ�� | �ϼ� | |
| 10����30�� | 50 | 10 | 60 |
| 30����50�� | 25 | 15 | 40 |
| �ϼ� | 75 | 25 | 100 |
���� ���⿼���˶����Լ������⣬Ҳ���������оٷ���ŵ���͵ĸ������⣬�ǻ�����Ŀ��


 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪a��b��ʵ����b��0������f��x��=1+asinbx��ͼ����ͼ��ʾ������������ĺ���y=loga��x+b����ͼ������ǣ�������
��֪a��b��ʵ����b��0������f��x��=1+asinbx��ͼ����ͼ��ʾ������������ĺ���y=loga��x+b����ͼ������ǣ�������| A�� | 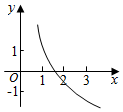 | B�� | 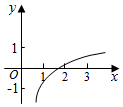 | C�� |  | D�� | 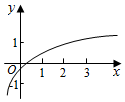 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ˫����x2-2y2=1�� | B�� | ��Բ${x^2}+\frac{y^2}{2}=1$�� | ||
| C�� | Բ${x^2}+{y^2}=\frac{1}{3}$�� | D�� | Բ${x^2}+{y^2}=\frac{2}{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֱ��a��b��ƽ����ͬһ��ƽ�� | B�� | ֱ��aƽ����ֱ��b���ڵ�ƽ�� | ||
| C�� | ֱ��a��b����ֱ��ͬһ��ֱ�� | D�� | ֱ��a��b����ֱ��ͬһ��ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��2 | B�� | a��2 | C�� | a��1 | D�� | a��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ijУ�����ȡ100��ѧ�����麮���ڼ�ѧ��ƽ��ÿ���ѧϰʱ�䣬�������ѧ��ÿ������ѧϰ��ʱ�����1Сʱ��11Сʱ֮�䣬��ѧ����ѧϰʱ��ֳ�5�飺��һ��[1��3�����ڶ���[3��5����������[5��7����������[7��9����������[9��11]�����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
ijУ�����ȡ100��ѧ�����麮���ڼ�ѧ��ƽ��ÿ���ѧϰʱ�䣬�������ѧ��ÿ������ѧϰ��ʱ�����1Сʱ��11Сʱ֮�䣬��ѧ����ѧϰʱ��ֳ�5�飺��һ��[1��3�����ڶ���[3��5����������[5��7����������[7��9����������[9��11]�����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1-i | B�� | 1+i | C�� | -1+i | D�� | 1-i |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com