练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．点（x，y）满足不等式|x|+|y|≤1，Z=（x-2）2+（y-2）2，则Z的最小值为$\frac{9}{2}$．

    分析 作出不等式组对应的平面区域，利用目标函数的几何意义进行求解即可．

    解答 解：不等式表示的平面区域为正方形ABCD及其内部，
    Z=（x-2）2+（y-2）2的几何意义表示为区域内的点到定点P（2，2）的距离的平方，
    由图象知作PE⊥AD，垂足为E，当E在线段AD上时，Z的最小值为|PE|2，
    可得|PE|2=$\frac{9}{2}$，
    故答案为：$\frac{9}{2}$．

    点评 本题主要考查二元一次不等式组表示平面区域的知识，以及线性规划的基本应用，利用数形结合是解决此类问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．分别取i，j为x轴、y轴正方向上的单位向量．若向量$\overrightarrow{a}$=x$\overrightarrow{i}$+y$\overrightarrow{j}$，则向量$\overrightarrow{a}$的坐标表示为（x，y）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若tan（π+α）=3，则sin（-α）cos（π-α）=（　　）
    A．$-\frac{3}{10}$B．$\frac{3}{10}$C．$-\frac{1}{10}$D．$\frac{1}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{m}$=1的一条渐近线的斜率的取值范围为（$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{5}}{2}$），求焦点在x轴上的椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1的离心率e的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知椭圆$C：\frac{x^2}{4}+{y^2}=1，A（{2，0}）$，点P在椭圆C上，且OP⊥PA，其中O为坐标原点，则点P的坐标为（　　）
    A．$（{\frac{2}{3}，±\frac{{2\sqrt{2}}}{3}}）$B．$（{\frac{{2\sqrt{5}}}{3}，±\frac{2}{3}}）$C．$（{-\frac{2}{3}，±\frac{{2\sqrt{2}}}{3}}）$D．$（{-\frac{{2\sqrt{5}}}{3}，±\frac{2}{3}}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知两条直线a，b和平面α，若a⊥b，b?α，则“a⊥α”是“b∥α”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设Sn是等差数列{an}的前n项和，若a2+a3+a4=3，则S5=（　　）
    A．5B．7C．9D．11

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

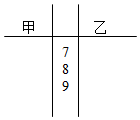    12．甲乙两组数学兴趣小组的同学举行了赛前模拟考试，成绩记录如下（单位：分）：
    甲：79，81，82，78，95，93，84，88
    乙：95，80，92，83，75，85，90，80
    （1）画出甲、乙两位学生成绩的茎叶图，；
    （2）计算甲、乙两组同学成绩的平均分和方差，并从统计学的角度分析，哪组同学在这次模拟考试中发挥比较稳定；
    （3）在甲、乙两组同学中，若对成绩不低于90分得再随机地抽3名同学进行培训，求抽出的3人中既有甲组同学又有乙组同学的概率．
    （参考公式：样本数据x1，x2，…，xn的标准差：
    s=$\sqrt{\frac{1}{n}[（{x}_{1}-\overline{x}）^{2}+（{x}_{2}-\overline{x}）^{2}+…+（{x}_{n}-\overline{x}）^{2}]}$，其中$\overline{x}$为样本平均数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

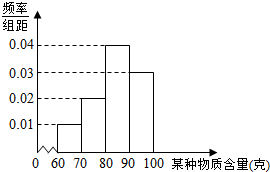    13．某企业对其生产的一批产品进行检测，得出每件产品中某种物质含量（单位：克）的频率分布直方图如图所示．
    （1）估计产品中该物质含量的中位数及平均数（同一组数据用该区间的中点值作代表）；
    （2）规定产品的级别如表：
    产品级别CBA
    某种物质含量范围[60，70）[70，80）[80，90）
    若生产1件A级品可获利润100元，生产1件B级品可获利润50元，生产1件C级品亏损50元．现管理人员从三个等级的产品中采用分层抽样的方式抽取10件产品，试用样本估计生产1件该产品的平均利润．

    查看答案和解析>>

    同步练习册答案