
| A. | f(x)=cos$\frac{πx}{3}$ | B. | $f(x)=sin\frac{πx}{3}$ | C. | f(x)=2cos2$\frac{πx}{6}$ | D. | f(x)=2cos2$\frac{πx}{12}$ |
分析 根据抽象函数关系结合函数奇偶性的性质求出f(3)=0,从而得到函数的周期是6,结合三角函数的周期性进行判断即可.
解答 解:∵f(x+6)=f(x)+f(3),
∴f(-3+6)=f(-3)+f(3),
∴f(-3)=0,函数f(x)是偶函数,
∴f(3)=0.
∴f(x+6)=f(x)+0=f(x),
∴f(x)是以6为周期的函数,
A.函数的周期T=$\frac{2π}{\frac{1}{3}π}$=6,f(3)=cosπ=-1,不满足条件f(3)=0.
B.$f(x)=sin\frac{πx}{3}$是奇函数,不满足条件.
C.f(x)=2cos2$\frac{πx}{6}$=1+cos$\frac{πx}{3}$,则函数的周期是T=$\frac{2π}{\frac{1}{3}π}$=6,f(3)=1+cosπ=1-1=0,满足条件.
D.f(x)=2cos2$\frac{πx}{12}$=1+cos$\frac{πx}{6}$,则函数的周期是T=$\frac{2π}{\frac{π}{6}}$=12,不满足条件.
故选:C.
点评 本题主要考查抽象函数的应用,根据函数的奇偶性得到函数的周期性,结合三角函数的周期性是解决本题的关键.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 双曲线x2-2y2=1上 | B. | 椭圆${x^2}+\frac{y^2}{2}=1$上 | ||
| C. | 圆${x^2}+{y^2}=\frac{1}{3}$上 | D. | 圆${x^2}+{y^2}=\frac{2}{3}$上 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{10}$ | B. | $\frac{3}{10}$ | C. | $-\frac{1}{10}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
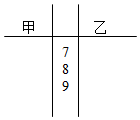 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com