Question

9．设函数f（x）=x²-ax，g（x）=|x-a|，其中a为实数．
（I）若f（x）+g（x）是偶函数，求实数a的值；
（Ⅱ）设t∈R，若?a∈[0，3]，对?x∈[0，3]，都有f（x）+l≥tg（x）成立，求实数t的最大值．

Answer 1

分析 （I）若f（x）+g（x）是偶函数，根据函数奇偶性的定义建立方程关系即可求实数a的值；
（Ⅱ）利用参数分离法转化为求函数的最值问题，利用分类讨论的思想进行求解．

解答 解：（I）设h（x）=f（x）+g（x）=x²-ax+|x-a|，
若h（x）是偶函数，
则h（-x）=h（x），
即x²+ax+|-x-a|=x²-ax+|x-a|，
即2ax=|x-a|-|x+a|，
令x=a，则a²=-|a|≥0，
则a=0，即实数a的值为0；
（Ⅱ）∵对?x∈[0，3]，都有f（x）+l≥tg（x）成立
∴g（x）=0时，即x=a时，满足条件．
若x≠a时，t≥（$\frac{1+f（x）}{g（x）}$）_min，
$\frac{1+f（x）}{g（x）}$=$\frac{{x}^{2}-ax+1}{|a-x|}$=$\left\{\begin{array}{l}{x-a+\frac{1}{x-a}+a，}&{a＜x≤3}\\{-（x-a）-\frac{1}{x-a}-a，}&{0≤x＜a}\end{array}\right.$，
令u=x-a，
则h（u）=$\left\{\begin{array}{l}{u+\frac{1}{u}+a，}&{0＜u≤3-a}\\{-u-\frac{1}{u}-a，}&{-a≤u＜0}\end{array}\right.$，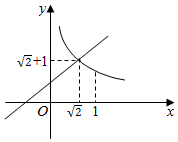
①当2＜a≤3时，h（u）_min=min{3+$\frac{1}{3-a}$，2-a}=2-a
②当1＜a≤2时，h（u）_min=min{2-a，2+a}=2-a，
此时存在实数a∈（1，3]，有t≤2-a，则t≤1，
③当0≤a＜1时，h（u）_min=min{2+a，$\frac{1}{a}$}如图：
要使垂直实数0≤a＜1时，t≤min{2+a，$\frac{1}{a}$}，
则需要t≤$\sqrt{2}+1$，即可，
综上实数t的最大值为$\sqrt{2}+1$．

点评 本题主要考查函数奇偶性的应用以及不等式恒成立问题，利用参数分离法转化为求函数的最值是解决本题的关键．综合性较强，难度较大．