
分析 (1)由离心率公式和点P满足椭圆方程,以及a,b,c的关系,解得a2=4,b2=3,由此能求出椭圆E的方程及直线AB的斜率;
(2)设AB的方程为y=-$\frac{1}{2}$x+t,代入椭圆方程得:x2-tx+t2-3=0,求得△=3(4-t2),运用韦达定理和弦长公式求得|AB|,运用点到直线的距离公式可得点P到直线AB的距离为d,求得S△PAB. 由此能求出△PAB的最大值和重心坐标.
解答 解:(1)由e=$\frac{c}{a}$=$\frac{1}{2}$,a2-b2=c2,
P在椭圆上,可得$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1,
解得a2=4,b2=3,
椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
设A(x1,y1)、B(x2,y2),
由$\overrightarrow{PA}$+$\overrightarrow{PB}$=m$\overrightarrow{OP}$,得
(x1+x2-2,y1+y2-3)=m(1,$\frac{3}{2}$),
即$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2+m}\\{{y}_{1}+{y}_{2}=3+\frac{3}{2}m}\end{array}\right.$,
又$\frac{{{x}_{1}}^{2}}{4}$+$\frac{1}{3}$y12=1,$\frac{{{x}_{2}}^{2}}{4}$+$\frac{1}{3}$y22=1,
两式相减得kAB=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=-$\frac{3}{4}$•$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$=-$\frac{3}{4}$•$\frac{2+m}{3+\frac{3}{2}m}$=-$\frac{1}{2}$;
(2)设AB的方程为y=-$\frac{1}{2}$x+t,
代入椭圆方程得:x2-tx+t2-3=0,
x1+x2=t,x1x2=t2-3,
△=3(4-t2),|AB|=$\sqrt{1+\frac{1}{4}}$•$\sqrt{{t}^{2}-4({t}^{2}-3)}$=$\frac{\sqrt{15}}{2}$•$\sqrt{4-{t}^{2}}$,
点P到直线AB的距离为d=$\frac{|4-2t|}{\sqrt{5}}$,
S△PAB=$\frac{1}{2}$d|AB|=$\frac{\sqrt{3}}{2}$|2-t|•$\sqrt{4-{t}^{2}}$=$\frac{1}{2}$$\sqrt{3(2-t)^{3}(2+t)}$(-2<t<2).
令f(t)=3(2-t)3(2+t),
则f’(t)=-12(2-t)2(t+1),
由f’(t)=0得t=-1或2(舍),
当-2<t<-1时,f’(t)>0,
当-1<t<2时f’(t)<0,
所以当t=-1时,f(t)有最大值81,
即△PAB的面积的最大值是$\frac{9}{2}$;
根据韦达定理得x1+x2=t=-1,
而x1+x2=2+m,所以2+m=-1,得m=-3,
于是x1+x2+1=3+m=0,y1+y2+$\frac{3}{2}$=3+$\frac{3m}{2}$+$\frac{3}{2}$=0,
因此△PAB的重心坐标为(0,0).
点评 本题考查椭圆方程的求法,注意运用离心率公式和点满足椭圆方程,考查直线斜率的计算,注意运用点差法,考查当△PAB的面积取得最大值时,原点O是△PAB的重心.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 双曲线x2-2y2=1上 | B. | 椭圆${x^2}+\frac{y^2}{2}=1$上 | ||
| C. | 圆${x^2}+{y^2}=\frac{1}{3}$上 | D. | 圆${x^2}+{y^2}=\frac{2}{3}$上 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组[1,3),第二组[3,5),第三组[5,7),第四组[7,9),第五组[9,11],绘制成如图所示的频率分布直方图.
某校随机抽取100名学生调查寒假期间学生平均每天的学习时间,被调查的学生每天用于学习的时间介于1小时和11小时之间,按学生的学习时间分成5组:第一组[1,3),第二组[3,5),第三组[5,7),第四组[7,9),第五组[9,11],绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
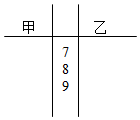 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
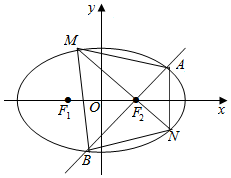 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,直线l经过F2且交椭圆C于A,B两点(如图),△ABF1的周长为4$\sqrt{2}$,原点O到直线l的最大距离为1.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,直线l经过F2且交椭圆C于A,B两点(如图),△ABF1的周长为4$\sqrt{2}$,原点O到直线l的最大距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com