
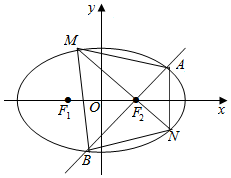
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,直线l经过F2且交椭圆C于A,B两点(如图),△ABF1的周长为4$\sqrt{2}$,原点O到直线l的最大距离为1.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,直线l经过F2且交椭圆C于A,B两点(如图),△ABF1的周长为4$\sqrt{2}$,原点O到直线l的最大距离为1.分析 (Ⅰ)由题意可得a,c的值,由隐含条件求得b的值,则椭圆方程可求;
(Ⅱ)分类求出直线AB的斜率不存在、斜率为0时的四边形AMBN面积,在设出斜率存在且不为0时的直线方程,联立直线方程和椭圆方程利用弦长公式求得|AB|、|MN|的长度,代入四边形面积公式,换元后利用配方法求得最值,同时得到边形AMBN面积最小时直线l的方程.
解答 解:(Ⅰ)由题意知,$4a=4\sqrt{2}$,c=1,
∴$a=\sqrt{2}$,
又∵a2=b2+c2,∴b=1,
∴椭圆C的标准方程为$\frac{x^2}{2}+{y^2}=1$;
(Ⅱ)当直线AB的斜率不存在时,
有$A({1,\frac{{\sqrt{2}}}{2}})$,$|{AB}|=\sqrt{2},|{MN}|=2\sqrt{2}$,∴$S=\frac{1}{2}|{AB}|•|{MN}|=2$;
当直线AB的斜率为0时,$|{AB}|=2\sqrt{2},|{MN}|=\sqrt{2}$,∴$S=\frac{1}{2}|{AB}|•|{MN}|=2$;
当直线AB的斜率存在且不为0时,
设直线AB的方程为y=k(x-1),则直线MN的方程为$y=-\frac{1}{k}({x-1})$,
联立$\left\{\begin{array}{l}y=k({x-1})\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$得:(2k2+1)x2-4k2x+2k2-2=0.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=\frac{4{k}^{2}}{1+2{k}^{2}},{x}_{1}{x}_{2}=\frac{2{k}^{2}-2}{1+2{k}^{2}}$,
∴|AB|=$\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}\sqrt{(\frac{4{k}^{2}}{1+2{k}^{2}})^{2}-4\frac{2{k}^{2}-2}{1+2{k}^{2}}}$=$\frac{2\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$.
同理|MN|=$\frac{2\sqrt{2}((-\frac{1}{k})^{2}+1)}{2(-\frac{1}{k})^{2}+1}=\frac{2\sqrt{2}({k}^{2}+1)}{{k}^{2}+2}$,
∴$S=\frac{1}{2}$|AB|•|MN|=$\frac{4({k}^{2}+1)^{2}}{(2{k}^{2}+1)({k}^{2}+2)}$,
令t=k2+1(t≥1),$S=4\frac{t^2}{{2{t^2}+t-1}}=4\frac{1}{{-{{({\frac{1}{t}-\frac{1}{2}})}^2}+\frac{9}{4}}}$,
当$\frac{1}{t}=\frac{1}{2}$.即k2+1=2,即k=±1时,${S_{min}}=\frac{16}{9}$.
此时设直线AB的方程为y=±(x-1).
点评 本题考查椭圆的简单性质,考查了椭圆标准方程的求法,考查直线与椭圆位置关系的应用,训练了利用配方法求函数的最值,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [0,1] | C. | (-1,0) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{4}$ | B. | $\frac{49}{9}$ | C. | $\frac{144}{25}$ | D. | $\frac{225}{49}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
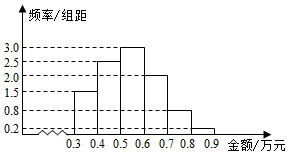 某电子商务公司随机抽取l000名网络购物者进行调查,这1000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),
某电子商务公司随机抽取l000名网络购物者进行调查,这1000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),| 购物金额分组 | [0.3,0.5) | [0.5,0.6) | [0.6,0.8) | [0.8,0.9] |
| 发放金额 | 50 | 100 | 150 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 1 | C. | 3 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com