
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点A1,A2,椭圆上不同于A1,A2的点P,A1P,A2P两直线的斜率之积为-$\frac{4}{9}$,△PA1A2面积最大值为6.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点A1,A2,椭圆上不同于A1,A2的点P,A1P,A2P两直线的斜率之积为-$\frac{4}{9}$,△PA1A2面积最大值为6.分析 (Ⅰ)设P(x,y),运用直线的斜率公式,以及椭圆的范围,求得三角形的最大面积,解方程可得a,b,进而得到椭圆方程;
(Ⅱ)设E的弦所在直线方程为y=-$\frac{x}{k}$+m,代入E的方程,得(4+$\frac{9}{{k}^{2}}$)x2-$\frac{18m}{k}$x+9m2-36=0,由此利用根的判别式、韦达定理结合已知条件能求出实数k的取值范围.
解答 解:(Ⅰ)设P(x,y),
椭圆的左右顶点A1(-a,0),A2(a,0),
由题意可得$\frac{y}{x+a}$•$\frac{y}{x-a}$=-$\frac{4}{9}$,
整理可得$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{\frac{4{a}^{2}}{9}}$=1,
即有b2=$\frac{4}{9}$a2,
△PA1A2面积最大值为6,
即有面积为S=$\frac{1}{2}$•2a•|yP|≤ab,
即S的最大值为ab=6,
解得a=3,b=2,
可得椭圆方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1;
(Ⅱ)设E的弦所在直线方程为y=-$\frac{x}{k}$+m,代入E的方程,得
(4+$\frac{9}{{k}^{2}}$)x2-$\frac{18m}{k}$x+9m2-36=0,
△=$\frac{324{m}^{2}}{{k}^{2}}$-4(4+$\frac{9}{{k}^{2}}$)(9m2-36)>0,
可得m2<4+$\frac{9}{{k}^{2}}$,①
设弦的两端为(x1,y1),(x2,y2),
则x1+x2=$\frac{18km}{9+4{k}^{2}}$,
弦的中点:x=$\frac{9km}{9+4{k}^{2}}$,y=-$\frac{9m}{9+4{k}^{2}}$+m=$\frac{4m{k}^{2}}{9+4{k}^{2}}$,
这个中点不在直线y=k(x-1)上,
∴$\frac{4m{k}^{2}}{9+4{k}^{2}}$≠k($\frac{9km}{9+4{k}^{2}}$-1),
即有m≠$\frac{9+4{k}^{2}}{5k}$,
m2≠$\frac{1}{25{k}^{2}}$(9+4k2)2,
由①可得,$\frac{(9+4{k}^{2})^{2}}{25{k}^{2}}$≥4+$\frac{9}{{k}^{2}}$
解得k≥2或k≤-2.
点评 本题考查点的轨迹方程的求法,考查满足条件的实数的取值范围的求法,解题时要认真审题,注意函数与方程思想的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
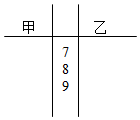 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):查看答案和解析>>
科目:高中数学 来源: 题型:解答题
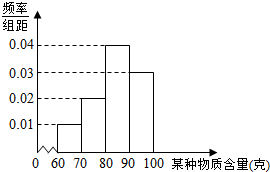 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.| 产品级别 | C | B | A |
| 某种物质含量范围 | [60,70) | [70,80) | [80,90) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.
如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
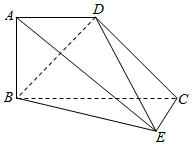 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com