练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】给出四个命题

    （1）若sin2A=sin2B，则△ABC为等腰三角形；

    （2）若sinA=cosB，则△ABC为直角三角形；

    （3）若sin2A+sin2B+sin2C＜2，则△ABC为钝角三角形；

    （4）若cos（A－B）cos（B－C）cos（C－A）=1，则△ABC为正三角形．

    以上正确命题的是_______．

    【答案】（3）（4）

    【解析】

    试题分析：（1）中满足或，所以三角形为等腰三角形或直角三角形；（2）中，但三角形不是直角三角形；（3）中由正弦定理

    ；（4）若cos（A-B）cos（B-C）cos（C-A）=1由三角函数的有界性可知三个都是1或者两个-1一个1都是1显然成立，如果两个-1又不可能，所以命题是三角形为正三角形的充要条件，所以（4）正确

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)＝|x－3|－|x＋1|，x∈R.

    (1)解不等式f(x)<－1；

    (2)设函数g(x)＝|x＋a|－4，且g(x)≤f(x)在x∈[－2，2]上恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝|2x－1|＋|x－2a|.

    (1)当a＝1时，求f(x)≤3的解集；

    (2)当x∈[1，2]时，f(x)≤3恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知幂函数(m∈Z)为偶函数，且在区间(0，＋∞)上是单调增函数．

    （1）求函数f(x)的解析式；

    （2）设函数，若g(x)>2对任意的x∈R恒成立，求实数c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x3+ax2+bx+a2.

    （I）若f（x）在x=1处有极值10，求a，b的值；

    （II）若当a=-1时，f（x）<0在x∈[1，2]恒成立，求b的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】本着健康、低碳的生活理念，租用公共自行车的人越来越多.租用公共自行车的收费标准是每车每次不超过两小时免费，超过两小时的部分每小时2元（不足1小时的部分按1小时计算）.甲乙两人相互独立租车（各租一车一次）.设甲、乙不超过两小时还车的概率分别为， ；两小时以上且不超过三小时还车的概率分别为， ；两人租车时间都不会超过四小时.

    （1）求出甲、乙所付租车费用相同的概率；

    （2）设甲、乙两人所付的租车费用之和为随机变量，求随机变量的概率分布和期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a是实数，函数f(x)＝ (x－a)．

    (1)求函数f(x)的单调区间；

    (2)设g(a)为f(x)在区间[0,2]上的最小值．

    ①写出g(a)的表达式；

    ②求a的取值范围，使得－6≤g(a)≤－2.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下是解决数学问题的思维过程的流程图：

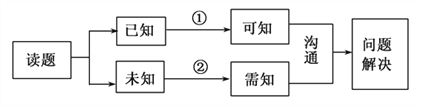
    在此流程图中，①、②两条流程线与“推理与证明”中的思维方法匹配正确的是( )

    A. ①—分析法，②—反证法 B. ①—分析法，②—综合法

    C. ①—综合法，②—反证法 D. ①—综合法，②—分析法

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数图象上点处的切线方程与直线平行（其中），.

    （Ⅰ）求函数的解析式；

    （Ⅱ）求函数在（）上的最小值；

    （Ⅲ）对一切， 恒成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案