
【题目】已知函数![]() 是定义域为
是定义域为![]() 上的奇函数,且
上的奇函数,且![]() .
.
(1)用定义证明:函数![]() 在
在![]() 上是增函数;
上是增函数;
(2)若实数t满足![]() 求实数t的范围.
求实数t的范围.
【答案】(1)见解析(2)(0,![]() )
)
【解析】
(1)由函数![]() 是定义域为(﹣1,1)上的奇函数,求出b=0,从而
是定义域为(﹣1,1)上的奇函数,求出b=0,从而![]() ,利用定义法能证明函数f(x)在(﹣1,1)上是增函数;
,利用定义法能证明函数f(x)在(﹣1,1)上是增函数;
(2)推导出f(2t﹣1)<f(1﹣t),由函数f(x)在(﹣1,1)上是增函数,列出不等式组,由此能求出实数t的范围.
解:(1)∵函数![]() 是定义域为(﹣1,1)上的奇函数,
是定义域为(﹣1,1)上的奇函数,
∴f(0)![]() 0,∴b=0,
0,∴b=0,
∴![]()
任取x1,x2∈(﹣1,1),且x1<x2,
∴f(x1)﹣f(x2)![]()
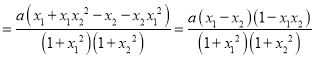 ,
,
∵a>0,﹣1<x1<x2<1,
∴x1﹣x2<0,1﹣x1x2>0,1![]() 0,1
0,1![]() 0,
0,
∴函数f(x)在(﹣1,1)上是增函数.
(2)∵f(2t﹣1)+f(t﹣1)<0,∴f(2t﹣1)<﹣f(t﹣1),
∵函数![]() 是定义域为(﹣1,1)上的奇函数,且a>0.
是定义域为(﹣1,1)上的奇函数,且a>0.
∴f(2t﹣1)<f(1﹣t),
∵函数f(x)在(﹣1,1)上是增函数,
∴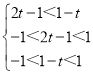 ,
,
解得0<t![]() .
.
故实数t的范围是(0,![]() ).
).


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,不可能成立的是()
,下列选项中,不可能成立的是()
A.![]() 没有最大元素,
没有最大元素, ![]() 有一个最小元素B.
有一个最小元素B.![]() 没有最大元素,
没有最大元素, ![]() 也没有最小元素
也没有最小元素
C.![]() 有一个最大元素,
有一个最大元素, ![]() 有一个最小元素D.
有一个最小元素D.![]() 有一个最大元素,
有一个最大元素, ![]() 没有最小元素
没有最小元素
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ).给你四个函数:①
).给你四个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)求函数![]() 的最小值;
的最小值;
(3)在给你的四个函数中,请选择一个函数(不需写出选择过程和理由),该函数记为![]() ,
,![]() 满足条件:存在实数a,使得关于x的不等式
满足条件:存在实数a,使得关于x的不等式![]() 的解集为
的解集为![]() ,其中常数s,
,其中常数s,![]() ,且
,且![]() .对选择的
.对选择的![]() 和任意
和任意![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与直线
与直线![]() 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若![]() 的面积是
的面积是![]() 面积的2倍,求
面积的2倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() ;
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 上的动点,当
上的动点,当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,人们对餐饮服务行业的要求也越来越高,由于工作繁忙无法抽出时间来享受美味,这样网上外卖订餐应运而生.若某商家的一款外卖便当每月的销售量![]() (单位:千盒)与销售价格
(单位:千盒)与销售价格![]() (单位:元/盒)满足关系式
(单位:元/盒)满足关系式![]() 其中
其中![]() ,
,![]() 为常数,已知销售价格为14元/盒时,每月可售出21千盒.
为常数,已知销售价格为14元/盒时,每月可售出21千盒.
(1)求![]() 的值;
的值;
(2)假设该款便当的食物材料、员工工资、外卖配送费等所有成本折合为每盒12元(只考虑销售出的便当盒数),试确定销售价格![]() 的值,使该店每月销售便当所获得的利润最大.(结果保留一位小数)
的值,使该店每月销售便当所获得的利润最大.(结果保留一位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com