
【题目】由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,不可能成立的是()
,下列选项中,不可能成立的是()
A.![]() 没有最大元素,
没有最大元素, ![]() 有一个最小元素B.
有一个最小元素B.![]() 没有最大元素,
没有最大元素, ![]() 也没有最小元素
也没有最小元素
C.![]() 有一个最大元素,
有一个最大元素, ![]() 有一个最小元素D.
有一个最小元素D.![]() 有一个最大元素,
有一个最大元素, ![]() 没有最小元素
没有最小元素
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a≠0),设函数y=[f(x)]2+pf(x)+q的零点所组成的集合为A,则以下集合不可能是A集合的序号为__.
①![]()
②![]()
③{﹣2,3,8}
④{﹣4,﹣1,0,2}
⑤{1,3,5,7}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
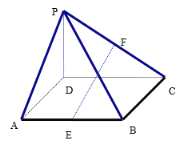
(1)求证:AB⊥平面PAD;
(2)求证:EF//平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月18日,举世瞩目的第18届亚运会在印尼首都雅加达举行,为了丰富亚运会志愿者的业余生活,同时鼓励更多的有志青年加入志愿者行列,大会主办方决定对150名志愿者组织一次有关体育运动的知识竞赛(满分120分)并计划对成绩前15名的志愿者进行奖励,现将所有志愿者的竞赛成绩制成频率分布直方图,如图所示,若第三组与第五组的频数之和是第二组的频数的3倍,试回答以下问题:
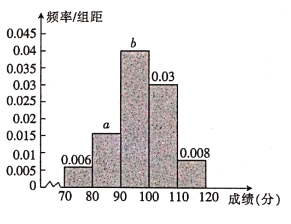
(1)求图中![]() 的值;
的值;
(2)求志愿者知识竞赛的平均成绩;
(3)从受奖励的15人中按成绩利用分层抽样抽取5人,再从抽取的5人中,随机抽取2人在主会场服务,求抽取的这2人中其中一人成绩在![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 上一点,
上一点,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,点
,点![]() 满足
满足![]() (
(![]() 为坐标原点),点
为坐标原点),点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,是否存在定点
,是否存在定点![]() ,使得直线
,使得直线![]() 、
、![]() 的斜率之和恒为0.若存在,则求出点
的斜率之和恒为0.若存在,则求出点![]() 的坐标;若不存在,则请说明理由.
的坐标;若不存在,则请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com