
【题目】已知点![]() 为圆
为圆![]() 上一点,
上一点,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,点
,点![]() 满足
满足![]() (
(![]() 为坐标原点),点
为坐标原点),点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,是否存在定点
,是否存在定点![]() ,使得直线
,使得直线![]() 、
、![]() 的斜率之和恒为0.若存在,则求出点
的斜率之和恒为0.若存在,则求出点![]() 的坐标;若不存在,则请说明理由.
的坐标;若不存在,则请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中作截面PQR,若PQ与CB的延长线交于点M,RQ与DB的延长线交于点N,RP与DC的延长线交于点K.
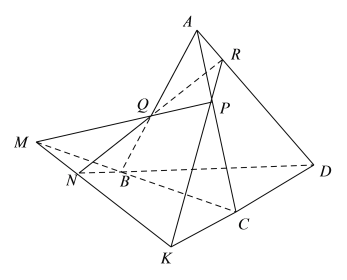
(1)求证:直线![]() 平面PQR;
平面PQR;
(2)求证:点K在直线MN上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,不可能成立的是()
,下列选项中,不可能成立的是()
A.![]() 没有最大元素,
没有最大元素, ![]() 有一个最小元素B.
有一个最小元素B.![]() 没有最大元素,
没有最大元素, ![]() 也没有最小元素
也没有最小元素
C.![]() 有一个最大元素,
有一个最大元素, ![]() 有一个最小元素D.
有一个最小元素D.![]() 有一个最大元素,
有一个最大元素, ![]() 没有最小元素
没有最小元素
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校为了对2018年录取的大一理工科新生有针对性地进行教学,从大一理工科新生中随机抽取40名,对他们2018年高考的数学分数进行分析,研究发现这40名新生的数学分数![]() 在
在![]() 内,且其频率
内,且其频率![]() 满足
满足![]() (其中
(其中![]() ,
,![]() ).
).

(1)求![]() 的值;
的值;
(2)请画出这20名新生高考数学分数的频率分布直方图,并估计这40名新生的高考数学分数的平均数(同一组中的数据用该组区间的中点值作代表);
(3)将此样本的频率估计为总体的概率,随机调查4名该校的大一理工科新生,记调查的4名大一理工科新生中“高考数学分数不低于130分”的人数为随机变量,求的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个人射击,甲射击一次中靶概率是![]() ,乙射击一次中靶概率是
,乙射击一次中靶概率是![]() .
.
(1)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(2)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)设![]() 个正数
个正数![]() 满足
满足![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,证明:
时,证明:![]() ;
;
(2)当![]() 时,不等式
时,不等式![]() 也成立,请你将其推广到
也成立,请你将其推广到![]() (
(![]() 且
且![]() )个正数
)个正数![]() 的情形,归纳出一般性的结论并用数学归纳法证明.
的情形,归纳出一般性的结论并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ).给你四个函数:①
).给你四个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)求函数![]() 的最小值;
的最小值;
(3)在给你的四个函数中,请选择一个函数(不需写出选择过程和理由),该函数记为![]() ,
,![]() 满足条件:存在实数a,使得关于x的不等式
满足条件:存在实数a,使得关于x的不等式![]() 的解集为
的解集为![]() ,其中常数s,
,其中常数s,![]() ,且
,且![]() .对选择的
.对选择的![]() 和任意
和任意![]() ,不等式
,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为![]() ,
,![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 与直线
与直线![]() 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若![]() 的面积是
的面积是![]() 面积的2倍,求
面积的2倍,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com