
【题目】已知函数f(x)=ax2+bx+c(a≠0),设函数y=[f(x)]2+pf(x)+q的零点所组成的集合为A,则以下集合不可能是A集合的序号为__.
①![]()
②![]()
③{﹣2,3,8}
④{﹣4,﹣1,0,2}
⑤{1,3,5,7}.
【答案】②④
【解析】
由题意将函数y=[f(x)]2+pf(x)+q的零点转化为f(x)=ax2+bx+c的函数值,根据二次函数的对称性即可判断.
f(x)=ax2+bx+c的对称轴为直线x=﹣![]() ,
,
设函数y=[f(x)]2+pf(x)+q的零点为y1,y2,
则必有y1=ax2+bx+c,y2=ax2+bx+c,
方程y1=ax2+bx+c的两个解x1,x2要关于直线x=﹣![]() 对称,
对称,
也就是说2(x1+x2)=﹣![]() ,
,
同理方程y2=ax2+bx+c的两个解x3,x4也要关于直线x=﹣![]() 对称
对称
那就得到2(x3+x4)=﹣![]() ,
,
①![]() 可以找到对称轴直线x=
可以找到对称轴直线x=![]()
②![]() 不能找到对称轴直线,
不能找到对称轴直线,
③{﹣2,3,8}可以找到对称轴直线x=3,
④{﹣4,﹣1,0,2}不能找到对称轴直线,
⑤{1,3,5,7}可以找到对称轴直线x=4,
故答案为:②④.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(ax2+x+6).
(1)若a=﹣1,求f(x)的定义域,并讨论f(x)的单调性;
(2)若函数f(x)的定义域为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线顶点在原点,焦点在x轴上,且过点(4,4),焦点为F.
(1)求抛物线的焦点坐标和标准方程;
(2)P是抛物线上一动点,M是PF的中点,求M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,g(x)=f(x)﹣3.
,g(x)=f(x)﹣3.
(1)判断并证明函数g(x)的奇偶性;
(2)判断并证明函数g(x)在(1,+∞)上的单调性;
(3)若f(m2﹣2m+7)≥f(2m2﹣4m+4)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中作截面PQR,若PQ与CB的延长线交于点M,RQ与DB的延长线交于点N,RP与DC的延长线交于点K.
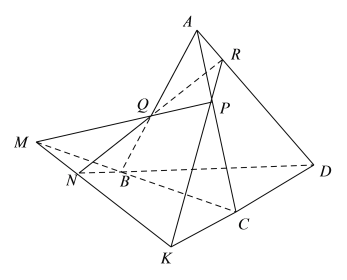
(1)求证:直线![]() 平面PQR;
平面PQR;
(2)求证:点K在直线MN上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,不可能成立的是()
,下列选项中,不可能成立的是()
A.![]() 没有最大元素,
没有最大元素, ![]() 有一个最小元素B.
有一个最小元素B.![]() 没有最大元素,
没有最大元素, ![]() 也没有最小元素
也没有最小元素
C.![]() 有一个最大元素,
有一个最大元素, ![]() 有一个最小元素D.
有一个最小元素D.![]() 有一个最大元素,
有一个最大元素, ![]() 没有最小元素
没有最小元素
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com