
【题目】设b和c分别是先后抛掷一颗骰子得到的点数,则方程x2﹣bx+c=0有实根的概率为 .
【答案】![]()
【解析】
试题由已知b2﹣4c≥0,b和c分别是先后抛掷一颗骰子得到的点数,基本事件总数n=6×6=36,再用列举法求出方程x2﹣bx+c=0有实根,即b2≥4c包含的基本事件个数,由此能求出方程x2﹣bx+c=0有实根的概率.
解:∵方程x2﹣bx+c=0有实根,
∴△=(﹣b)2﹣4c=b2﹣4c≥0,
∵b和c分别是先后抛掷一颗骰子得到的点数,
∴基本事件总数n=6×6=36,
方程x2﹣bx+c=0有实根,即b2≥4c包含的基本事件情况有:
b=2时,c可取1;b=3时,c可取1,2;b=4时,c可取1,2,3,4;
b=5时,c可取1,2,3,4,5,6;b=6时,c可取1,2,3,4,5,6,
∴方程x2﹣bx+c=0有实根,即b2≥4c包含的基本事件个数m=1+2+4+6+6=19,
∴方程x2﹣bx+c=0有实根的概率p=![]() =
=![]() .
.
故答案为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点, ![]() 为椭圆
为椭圆![]() 的上顶点,点
的上顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() 为坐标原点,且
为坐标原点,且![]() ,
, ![]() .
.
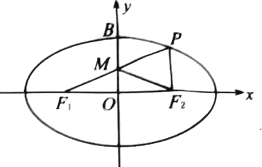
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线分别与椭圆
作两条互相垂直的直线分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点(异于点
两点(异于点![]() ),证明:直线
),证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图,估计这次数学竞赛的及格率(60分及以上为及格)是( )

A. 0.9 B. 0.75 C. 0.8 D. 0.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学纳法证明你的猜想,并求出an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为3的等边三角形,四边形
是边长为3的等边三角形,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .点
.点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,点
,点![]() 为
为![]() 上的一点,且
上的一点,且![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,在直四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA
中,底面ABCD为等腰梯形,AB//CD,AB=4,BC=CD=2,AA![]() =2,E、E
=2,E、E![]() 分别是棱AD、AA
分别是棱AD、AA![]() 的中点.
的中点.

(1)设F是棱AB的中点,证明:直线EE![]() //平面FCC
//平面FCC![]() ;
;
(2)证明:平面D1AC⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底,
为自然对数的底, ![]() )的导函数为
)的导函数为![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)设点![]() ,
, ![]() 是函数
是函数![]() 图象上两点,若对任意的
图象上两点,若对任意的![]() ,割线
,割线![]() 的斜率都大于
的斜率都大于![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在某商业区周边有 两条公路![]() 和
和![]() ,在点
,在点![]() 处交汇,该商业区为圆心角
处交汇,该商业区为圆心角![]() ,半径3
,半径3![]() 的扇形,现规划在该商业区外修建一条公路
的扇形,现规划在该商业区外修建一条公路![]() ,与
,与![]() ,
,![]() 分别交于
分别交于![]() ,要求
,要求![]() 与扇形弧相切,切点
与扇形弧相切,切点![]() 不在
不在![]() ,
,![]() 上.
上.
(1)设![]() 试用
试用![]() 表示新建公路
表示新建公路![]() 的长度,求出
的长度,求出![]() 满足的关系式,并写出
满足的关系式,并写出![]() 的范围;
的范围;
(2)设![]() ,试用
,试用![]() 表示新建公路
表示新建公路![]() 的长度,并且确定
的长度,并且确定![]() 的位置,使得新建公路
的位置,使得新建公路![]() 的长度最短.
的长度最短.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com