
【题目】如图,已知![]() ,
, ![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点, ![]() 为椭圆
为椭圆![]() 的上顶点,点
的上顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() 为坐标原点,且
为坐标原点,且![]() ,
, ![]() .
.
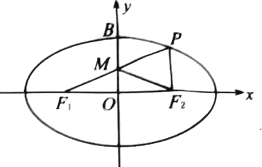
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线分别与椭圆
作两条互相垂直的直线分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点(异于点
两点(异于点![]() ),证明:直线
),证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,  .
.
【解析】试题分析:
(1)由题意可得![]() 为
为![]() 的中位线,从而可得
的中位线,从而可得![]() ,故
,故![]() ,且
,且![]() ,然后根据
,然后根据![]() 和
和![]() 可得
可得![]() ,
, ![]() ,由此可得椭圆的方程.(2)分别设出直线直线
,由此可得椭圆的方程.(2)分别设出直线直线![]() 的方程,解方程组可得点
的方程,解方程组可得点![]() ,
, ![]() 的坐标,经分析题意可得定点必在
的坐标,经分析题意可得定点必在![]() 轴上,不妨设该点坐标
轴上,不妨设该点坐标![]() ,然后根据直线
,然后根据直线![]() 的斜率相等建立关于
的斜率相等建立关于![]() 的等式,结合点
的等式,结合点![]() ,
, ![]() 的坐标经计算可得定点坐标.
的坐标经计算可得定点坐标.
试题解析:
(1)由题意得![]() ,
,
∴![]() 为
为![]() 的中位线,
的中位线,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴椭圆方程为![]() .
.
(2)设![]() ,
, ![]() ,直线
,直线![]() :
: ![]() ,
,
由 消去y整理得
消去y整理得![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() ,
,
以![]() 代替上式中的
代替上式中的![]() ,可得
,可得 .
.
由题意可得,若直线![]() 关于
关于![]() 轴对称后得到直线
轴对称后得到直线![]() ,
,
则得到的直线![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,
所以若直线![]() 经过定点,该定点一定是直线
经过定点,该定点一定是直线![]() 与
与![]() 的交点,故该点必在
的交点,故该点必在![]() 轴上.
轴上.
设该点坐标![]() ,则有
,则有![]() ,
,
∴![]()
 ,
,
将![]() 的值代入上式,化简得
的值代入上式,化简得![]() ,
,
∴直线![]() 经过定点
经过定点 .
.


科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: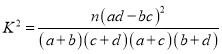 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于疫情影响,今年我们学校开展线上教学,高一年级某班班主任为了了解学生上网学习时间,对本班40名学生某天上网学习时间进行了调查,将数据(取整数)整理后,绘制出如图所示频率分布直方图,已知从左到右各个小组的频率分别是0.15,0.25,0.35,0.20,0.05,则根据直方图所提供的信息.

(1)这一天上网学习时间在![]() 分钟之间的学生有多少人?
分钟之间的学生有多少人?
(2)这40位同学的线上平均学习时间是多少?
(3)如果只用这40名学生这一天上网学习时间作为样本去推断该校高一年级全体学生该天的上网学习时间,这样推断是否合理?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知扇形的圆心角是α,半径为R,弧长为l.
(1)若α=75°,R=12 cm,求扇形的弧长l和面积;
(2)若扇形的周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列抽取样本的方式属于简单随机抽样的个数为( )
①从无限多个个体中抽取100个个体作为样本.
②盒子里共有80个零件,从中选出5个零件进行质量检验.在抽样操作时,从中任意拿出一个零件进行质量检验后再把它放回盒子里.
③从20件玩具中一次性抽取3件进行质量检验.
④某班有56名同学,指定个子最高的5名同学参加学校组织的篮球赛.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·长沙二模)在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则![]() .推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则
.推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则![]() =________.
=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业2017年招聘员工,其中A、B、C、D、E五种岗位的应聘人数、录用人数和录用比例(精确到1%)如下:

(Ⅰ)从表中所有应聘人员中随机选择1人,试估计此人被录用的概率;
(Ⅱ)从应聘E岗位的6人中随机选择1名男性和1名女性,求这2人均被录用的概率;
(Ⅲ)表中A、B、C、D、E各岗位的男性、女性录用比例都接近(二者之差的绝对值不大于5%),但男性的总录用比例却明显高于女性的总录用比例.研究发现,若只考虑其中某四种岗位,则男性、女性的总录用比例也接近,请写出这四种岗位.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型活动即将举行,为了做好接待工作,组委会招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有![]() 人和
人和![]() 人喜爱运动,其余人不喜爱运动.
人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下![]() 列联表:
列联表:
喜爱运动 | 不喜爱运动 | 总计 | |
男志愿者 | |||
女志愿者 | |||
总计 |
(2)根据列联表判断能否有![]() ℅的把握认为性别与喜爱运动有关?
℅的把握认为性别与喜爱运动有关?
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com