
【题目】(2018·长沙二模)在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则![]() .推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则
.推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则![]() =________.
=________.
科目:高中数学 来源: 题型:
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 平面
平面![]() .
.
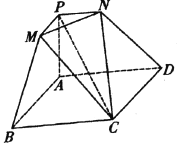
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司近年来特别注重创新产品的研发,为了研究年研发经费![]() (单位:万元)对年创新产品销售额
(单位:万元)对年创新产品销售额![]() (单位:十万元)的影响,对近10年的研发经费
(单位:十万元)的影响,对近10年的研发经费![]() 与年创新产品销售额
与年创新产品销售额![]() (其中
(其中![]() )的数据作了初步处理,得到如图的散点图及一些统计量的值.
)的数据作了初步处理,得到如图的散点图及一些统计量的值.
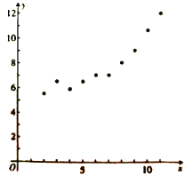
其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .现拟定
.现拟定![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(1)求![]() ,
,![]() 的值(结果精确到
的值(结果精确到![]() );
);
(2)根据拟定的回归方程,预测当研发经费为![]() 万元时,年创新产品销售额是多少?
万元时,年创新产品销售额是多少?
参考公式:
求线性回归方程系数公式 :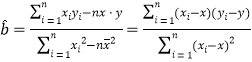 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
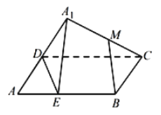
【题目】如图,矩形![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转为
翻转为![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻转过程中,有下列命题:
翻转过程中,有下列命题:
①![]() 是定值;
是定值;
②点![]() 在圆上运动;
在圆上运动;
③一定存在某个位置,使![]() ;
;
④若![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() .
.
其中正确的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
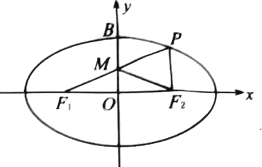
【题目】如图,已知![]() ,
, ![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点, ![]() 为椭圆
为椭圆![]() 的上顶点,点
的上顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() 为坐标原点,且
为坐标原点,且![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线分别与椭圆
作两条互相垂直的直线分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点(异于点
两点(异于点![]() ),证明:直线
),证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】流行性感冒多由病毒引起,据调查,空气相对湿度过大或过小时,都有利于一些病毒的繁殖和传播.科学测定,当空气相对湿度大于65%或小于40%时,病毒繁殖滋生较快,当空气相对湿度在45%—55%时,病毒死亡较快,现随机抽取了全国部分城市,获得了它们的空气月平均相对湿度共300个数据,整理得到数据分组及频数分布表,其中为了记录方便,将空气相对湿度在![]() %~
%~![]() %时记为区间
%时记为区间![]() .
.

(I)求上述数据中空气相对湿度使病毒死亡较快的频率;
(Ⅱ)从区间[ 15,35)的数据中任取两个数据,求恰有一个数据位于[25,35)的概率;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中空气月平均相对湿度的平均数在第几组(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在即将进入休渔期时,某小微企业决定囤积一些冰鲜产品,销售所囤积产品的净利润f(x)万元与投入x万元之间近似满足函数关系: ,若投入2万元,可得到净利润为5.2万元.
,若投入2万元,可得到净利润为5.2万元.
(1)试求该小微企业投入多少万元时,获得的净利润最大;
(2)请判断该小微企业是否会亏本,若亏本,求出投入资金的范围,若不亏本,请说明理由.(参考数据:ln 2≈0.7,ln 15≈2.7)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为3的等边三角形,四边形
是边长为3的等边三角形,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .点
.点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,点
,点![]() 为
为![]() 上的一点,且
上的一点,且![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com