
【题目】某公司近年来特别注重创新产品的研发,为了研究年研发经费![]() (单位:万元)对年创新产品销售额
(单位:万元)对年创新产品销售额![]() (单位:十万元)的影响,对近10年的研发经费
(单位:十万元)的影响,对近10年的研发经费![]() 与年创新产品销售额
与年创新产品销售额![]() (其中
(其中![]() )的数据作了初步处理,得到如图的散点图及一些统计量的值.
)的数据作了初步处理,得到如图的散点图及一些统计量的值.
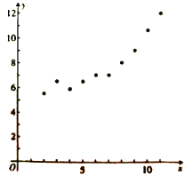
其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .现拟定
.现拟定![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(1)求![]() ,
,![]() 的值(结果精确到
的值(结果精确到![]() );
);
(2)根据拟定的回归方程,预测当研发经费为![]() 万元时,年创新产品销售额是多少?
万元时,年创新产品销售额是多少?
参考公式:
求线性回归方程系数公式 :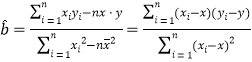 ,
,![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率是
的离心率是![]() ,一个顶点是
,一个顶点是![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,且
的任意两点,且![]() .试问:直线
.试问:直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 分別为棱
分別为棱![]() 的中点
的中点

(1)求三棱柱![]() 的体积;
的体积;
(2)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:

根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于疫情影响,今年我们学校开展线上教学,高一年级某班班主任为了了解学生上网学习时间,对本班40名学生某天上网学习时间进行了调查,将数据(取整数)整理后,绘制出如图所示频率分布直方图,已知从左到右各个小组的频率分别是0.15,0.25,0.35,0.20,0.05,则根据直方图所提供的信息.

(1)这一天上网学习时间在![]() 分钟之间的学生有多少人?
分钟之间的学生有多少人?
(2)这40位同学的线上平均学习时间是多少?
(3)如果只用这40名学生这一天上网学习时间作为样本去推断该校高一年级全体学生该天的上网学习时间,这样推断是否合理?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,其中一个焦点与抛物线
的中心在原点,其中一个焦点与抛物线![]() 的焦点重合,点
的焦点重合,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆的左右焦点分别为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求以
,求以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知扇形的圆心角是α,半径为R,弧长为l.
(1)若α=75°,R=12 cm,求扇形的弧长l和面积;
(2)若扇形的周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·长沙二模)在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则![]() .推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则
.推广到空间可以得到类似结论:已知正四面体P-ABC的内切球体积为V1,外接球体积为V2,则![]() =________.
=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果双曲线的离心率e=![]() ,则称此双曲线为黄金双曲线.有以下几个命题:①双曲线
,则称此双曲线为黄金双曲线.有以下几个命题:①双曲线![]() 是黄金双曲线;②双曲线
是黄金双曲线;②双曲线![]() 是黄金双曲线;③在双曲线
是黄金双曲线;③在双曲线![]() (a>0,b>0)中,F1为左焦点,A2为右顶点,B1(0,b),若∠F1B1A2=90°,则该双曲线是黄金双曲线;④在双曲线
(a>0,b>0)中,F1为左焦点,A2为右顶点,B1(0,b),若∠F1B1A2=90°,则该双曲线是黄金双曲线;④在双曲线![]() (a>0,b>0)中,过右焦点F2作实轴的垂线交双曲线于M,N两点,O为坐标原点,若∠MON=120°,则该双曲线是黄金双曲线.其中正确命题的序号为________.
(a>0,b>0)中,过右焦点F2作实轴的垂线交双曲线于M,N两点,O为坐标原点,若∠MON=120°,则该双曲线是黄金双曲线.其中正确命题的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com