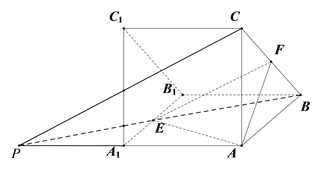
【题目】如图，在三棱柱
中，侧面
底面
，
，
，
分別为棱
的中点
（1）求三棱柱的体积；
（2）在直线
上是否存在一点
，使得
平面
？若存在，求出
的长；若不存在，说明理由.
【答案】（1）
；（2）
.
【解析】试题分析：（1）第（1）问，先证明
底面ABC,计算出△ABC的面积，再利用柱体的体积公式求三棱柱
的体积.(2)第(2)问，先假设在直线
上存在点P，使得CP||平面AEF，再找到点P的位置，再求AP的长.
试题解析：
（1）三棱柱中，所以
.
因为
，所以
.
又因为
，
连接
,所以△
是边长为2的正三角形.
因为E是棱
的中点，所以
，且
又
，所以
又侧面
底面ABC，且侧面
底面ABC=AB，
又AE
侧面
，所以底面ABC，
所以三棱柱的体积为
；
（2）在直线上存在点P，使得CP||平面AEF.
证明如下：连接
并延长，与的延长线相交，设交点为
.连接
.
因为
，故
由于
为棱的中点，所以
，故有
又
为棱
的中点，故
为
的中位线，所以
又
平面AEF，
平面AEF， 所以
平面AEF.
故在直线上存在点P，使得平面AEF.
此时，
所以
.
科目：高中数学 来源： 题型：
【题目】质检部门对某工厂甲、乙两个车间生产的
个零件质量进行检测．甲、乙两个车间的零件质量（单位：克）分布的茎叶图如图所示．零件质量不超过
克的为合格．
（1）质检部门从甲车间
个零件中随机抽取
件进行检测，若至少
件合格，检测即可通过，若至少
件合格，检测即为良好，求甲车间在这次检测通过的条件下，获得检测良好的概率；
（2）若从甲、乙两车间个零件中随机抽取个零件，用
表示乙车间的零件个数，求的分布列与数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
，圆
.
（1）若直线
过点
且到圆心
的距离为
，求直线的方程；
（2）设过点
的直线
与圆交于
、
两点（的斜率为负），当
时，求以线段
为直径的圆的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示的几何体是由棱台
和棱锥
拼接而成的组合体，其底面四边形
是边长为2的菱形，
，
平面
.
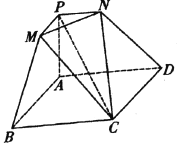
（1）求证：
；
（2）求平面
与平面
所成锐角二面角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知曲线
的极坐标方程为
，直线
：
，直线
：
.以极点
为原点，极轴为
轴的正半轴建立平面直角坐标系.
（1）求直线，的直角坐标方程以及曲线的参数方程；
（2）已知直线与曲线交于，
两点，直线与曲线交于，
两点，求
的面积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设z1是虚数，z2＝z1
是实数，且﹣1≤z2≤1．
（1）求|z1|的值以及z1的实部的取值范围；
（2）若ω
，求证ω为纯虚数；
（3）求z2﹣ω2的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司近年来特别注重创新产品的研发，为了研究年研发经费
(单位：万元)对年创新产品销售额
(单位：十万元)的影响，对近10年的研发经费
与年创新产品销售额
（其中
）的数据作了初步处理，得到如图的散点图及一些统计量的值.
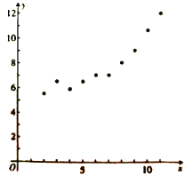
其中
，
，
，
，
.现拟定关于的回归方程为
.
（1）求
，
的值(结果精确到
)；
（2）根据拟定的回归方程,预测当研发经费为
万元时,年创新产品销售额是多少？
参考公式：
求线性回归方程系数公式 ：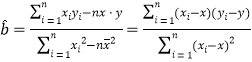
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在即将进入休渔期时，某小微企业决定囤积一些冰鲜产品，销售所囤积产品的净利润f(x)万元与投入x万元之间近似满足函数关系：
，若投入2万元，可得到净利润为5.2万元．
(1)试求该小微企业投入多少万元时，获得的净利润最大；
(2)请判断该小微企业是否会亏本，若亏本，求出投入资金的范围，若不亏本，请说明理由．(参考数据：ln 2≈0.7，ln 15≈2.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
