
分析 把函数看作是动点M(x,e2x)与动点N(a,2a)之间距离的平方,利用导数求出曲线y=e2x上与直线y=2x平行的切线的切点,得到曲线上点到直线距离的最小值,结合题意可得只有切点到直线距离的平方等于$\frac{1}{5}$,然后由两直线斜率的关系列式求得实数a的值.
解答 解:函数f(x)=e2x(e2x-4a)+x(x-2a)+5a2=(e2x-2a)2+(x-a)2,
函数f(x)可以看作是动点M(x,e2x)与动点N(a,2a)之间距离的平方,
动点M在函数y=e2x的图象上,N在直线y=2x的图象上,
问题转化为求直线上的动点到曲线的最小距离,
由y=e2x得,y'=2e2x=2,解得x=0,
∴曲线上点M(0,1)到直线y=2x的距离最小,
最小距离d=$\frac{1}{\sqrt{5}}$,
则f(x)≥$\frac{1}{5}$,
根据题意,要使f(x0)≤$\frac{1}{5}$,
则f(x0)=$\frac{1}{5}$,此时N恰好为垂足,
由kMN=$\frac{2a-1}{a}$=-$\frac{1}{2}$,
解得a=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$
点评 本题考查利用导数求曲线上过某点切线的斜率,考查了数形结合和数学转化思想方法,训练了点到直线的距离公式的应用,是中档题.


科目:高中数学 来源: 题型:解答题
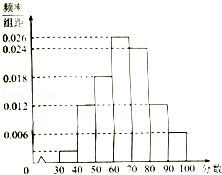 某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b=48 | 60 |
| 女生 | c=6 | d=34 | 40 |
| 合计 | 18 | 82 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 产量每增加1000件,单位成本下降2.13元 | |
| B. | 产量每减少1000件,单位成本下降2.13元 | |
| C. | 产量每增加1000件,单位成本上升2130元 | |
| D. | 产量每减少1000件,单位成本上升2130元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ∈(0,1) | B. | λ∈(-1,0) | C. | λ∈(0,$\frac{\sqrt{2}}{2}$) | D. | λ∈(-$\frac{\sqrt{2}}{2}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,点A在平面A1BC中的投影为线段A1B上的点D.
如图所示,在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,点A在平面A1BC中的投影为线段A1B上的点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com