
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
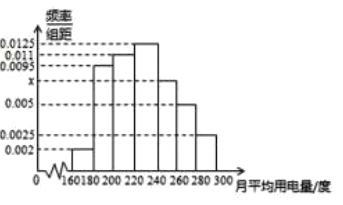
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量在![]() ,
, ![]() ,
, ![]() 的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在
的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
【答案】(1)0.0075;(2)224;(3)5.
【解析】试题分析:(1)由频率和为1,计算图中x的值;(2)根据频率分布直方图观察,最高矩形的中点横坐标即为众数,令矩形面积和为![]() ,所取得的横坐标为中位数;(3)分别计算出月平均用电量在
,所取得的横坐标为中位数;(3)分别计算出月平均用电量在![]() ,
, ![]() ,
, ![]() 的三组用户的数量,根据分层抽样的定义计算出抽取比例,得出月平均用电量在
的三组用户的数量,根据分层抽样的定义计算出抽取比例,得出月平均用电量在![]() 的用户中应抽取的户数.
的用户中应抽取的户数.
试题解析:
(1)由直方图的性质,可得![]() ,
, ![]() ,所以直方图中
,所以直方图中![]() 的值是
的值是![]() .
.
(2)月平均用电量的众数是![]() .
.
因为![]() ,
,
所以月平均用电量的中位数在![]() 内,
内,
设中位数为![]() ,由
,由![]() ,得
,得![]() ,
,
所以月平均用电量的中位数是224.
(3)月平均用电量为![]() 的用户有
的用户有![]() 户,
户,
月平均用电量为![]() 的用户有
的用户有![]() 户,
户,
月平均用电量为![]() 的用户有
的用户有![]() 户,
户,
抽取比例![]() ,
,
所以月平均用电量在![]() 的用户中应抽取
的用户中应抽取![]() 户.
户.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
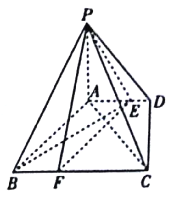
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时, ![]() (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, ![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共![]() 个,生产一个卫兵需
个,生产一个卫兵需![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润![]() 元.
元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下图中,四边形 ABCD是等腰梯形, ![]() ,
, ![]() ,O、Q分别为线段AB、CD的中点,OQ与EF的交点为P,OP=1,PQ=2,现将梯形ABCD沿EF折起,使得
,O、Q分别为线段AB、CD的中点,OQ与EF的交点为P,OP=1,PQ=2,现将梯形ABCD沿EF折起,使得![]() ,连结AD、BC,得一几何体如图所示.
,连结AD、BC,得一几何体如图所示.
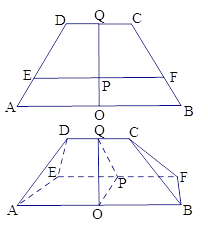
(Ⅰ)证明:平面ABCD![]() 平面ABFE;
平面ABFE;
(Ⅱ)若上图中, ![]() ,CD=2,求平面ADE与平面BCF所成锐二面角的余弦值.
,CD=2,求平面ADE与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
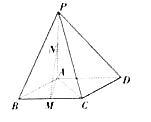
【题目】如图:在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点,且
的中点,且![]() .
.
(1)证明: ![]() 面
面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ;若存在,求出
;若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市两所高中分别组织部分学生参加了“七五普法网络知识大赛”,现从这两所学校的参赛学生中分别随机抽取30名学生的成绩(百分制)作为样本,得到样本数据的茎叶图如图所示.
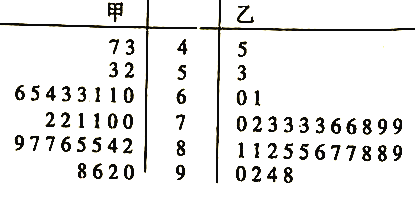
(Ⅰ)若乙校每位学生被抽取的概率为0.15,求乙校参赛学生总人数;
(Ⅱ)根据茎叶图,从平均水平与波动情况两个方面分析甲、乙两校参赛学生成绩(不要求计算);
(Ⅲ)从样本成绩低于60分的学生中随机抽取3人,求3人不在同一学校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x2﹣1)=loga ![]() (a>0且a≠1)
(a>0且a≠1)
(1)求函数f(x)的解析式,并判断f(x)的奇偶性;
(2)解关于x的方程f(x)=loga ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com