
分析 分别求出使命题p,q为真时,x的取值范围,进而根据¬p是¬q的充分而不必要条件,构造不等式组,解得实数m的取值范围.
解答 解:∵|1-$\frac{x-1}{3}}$|≤2,
∴-2≤1-$\frac{x-1}{3}}$≤2,
∴-3≤-$\frac{x-1}{3}}$≤1,
∴-3≤x-1≤9,
∴-2≤x≤10,
即命题p:-2≤x≤10,
故命题¬p:x<-2,或x>10,
∵命题q:1-m≤x≤1+m(m>0),
∴命题¬q:x<1-m,或x>1+m,(m>0),
∵¬p是¬q的充分而不必要条件,
∴$\left\{\begin{array}{l}-2≤1-m\\ 10≥1+m\\ m>0\end{array}\right.$,
解得:0<m≤3
点评 本题以命题的真假判断与应用为载体,考查了充要条件,不等式的解法等知识点,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
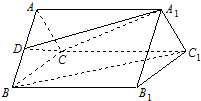 如图,在正三棱柱ABC-A1B1C1中,点D是棱AB的中点,BC=1,AA1=$\sqrt{3}$.
如图,在正三棱柱ABC-A1B1C1中,点D是棱AB的中点,BC=1,AA1=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
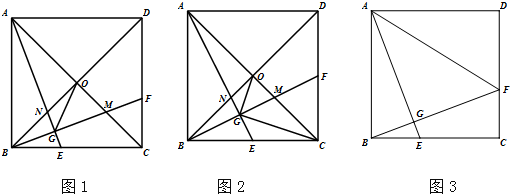
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
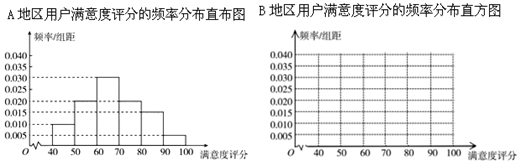
| 满意度 评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 2 | 8 | 14 | 10 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com