
【题目】随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限![]() 与所支出的总费用
与所支出的总费用![]() (万元)有如表的数据资料:
(万元)有如表的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1) 在给出的坐标系中作出散点图;
(2)求线性回归方程![]() 中的
中的![]() 、
、![]() ;
;
(3)估计使用年限为![]() 年时,车的使用总费用是多少?
年时,车的使用总费用是多少?
(最小二乘法求线性回归方程系数公式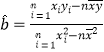 ,
, ![]() .)
.)
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】在某校组织的高二女子排球比赛中,有![]() 、
、![]() 两个球队进入决赛,决赛采用7局4胜制.假设
两个球队进入决赛,决赛采用7局4胜制.假设![]() 、
、![]() 两队在每场比赛中获胜的概率都是
两队在每场比赛中获胜的概率都是![]() .并记需要比赛的场数为
.并记需要比赛的场数为![]() .
.
(Ⅰ)求![]() 大于4的概率;
大于4的概率;
(Ⅱ)求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,H是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口H是
,H是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口H是![]() 的中点,点E,F分别落在线段
的中点,点E,F分别落在线段![]() 上.已知
上.已知![]() ,记
,记![]() .
.

(1)试将污水管道的长度表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)已知![]() ,求此时管道的长度l;
,求此时管道的长度l;
(3)当![]() 取何值时,铺设管道的成本最低?并求出此时管道的长度.
取何值时,铺设管道的成本最低?并求出此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,离心率
,离心率![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,则
,则![]() 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() .直角梯形
.直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且使得平面
为轴旋转得到,且使得平面![]() 平面
平面![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)延长![]() 至点
至点![]() ,使
,使![]() 为平面
为平面![]() 内的动点,若直线
内的动点,若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,且
,且![]() ,求点
,求点![]() 到点
到点![]() 的距离的最小值.
的距离的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若数列![]() 和
和![]() 满足
满足![]() 则称数列
则称数列![]() 是数列
是数列![]() 的“伴随数列”.
的“伴随数列”.
已知数列![]() 是数列
是数列![]() 的伴随数列,试解答下列问题:
的伴随数列,试解答下列问题:
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() ;
;
(2)若![]() ,
,![]() 为常数,求证:数列
为常数,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,数列
,数列![]() 是等比数列,求
是等比数列,求![]() 的数值.
的数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三次函数f(x)=ax3+bx2+cx+1的导函数为f![]() (x)=3ax(x-2),若函数y=f(x)共有三个不同的零点,则a的取值范围是( )
(x)=3ax(x-2),若函数y=f(x)共有三个不同的零点,则a的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 分别是椭圆
分别是椭圆![]()
![]() 的长轴端点、短轴端点,
的长轴端点、短轴端点,![]() 为坐标原点,若
为坐标原点,若![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如果斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() (都不同于点
(都不同于点![]() ),线段
),线段![]() 的中点为
的中点为![]() ,设线段
,设线段![]() 的垂线
的垂线![]() 的斜率为
的斜率为![]() ,试探求
,试探求![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com