
【题目】下列结论中正确的个数为( )
(1)![]() 是直线
是直线![]() 和直线
和直线![]() 垂直的充要条件;
垂直的充要条件;
(2)在线性回归方程中,相关系数![]() 越大,变量间的相关性越强;
越大,变量间的相关性越强;
(3)已知随机变量![]() ,若
,若![]() ,则
,则![]()
(4)若命题![]() ,
,![]() ,则
,则![]() ,
,![]()
A.1B.2C.3D.4
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点的坐标为
的右焦点的坐标为![]() ,且长轴长为短轴长的
,且长轴长为短轴长的![]() 倍.椭圆
倍.椭圆![]() 的上、下顶点分别为
的上、下顶点分别为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点(不同于
两点(不同于![]() 两点).
两点).
(1)求椭圆的方程;
(2)若直线![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)设直线![]() 相交于点
相交于点![]() ,求证:
,求证:![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代的四书是指:《大学》、《中庸》、《论语》、《孟子》,甲、乙、丙、丁![]() 名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则
名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则![]() 名同学所有可能的选择有______种.
名同学所有可能的选择有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蜂巢是由工蜂分泌蜂蜡建成的.从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成.如图,在正六棱柱![]() 的三个顶点
的三个顶点![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构,如下图(4)所示,
,就形成了蜂巢的结构,如下图(4)所示,
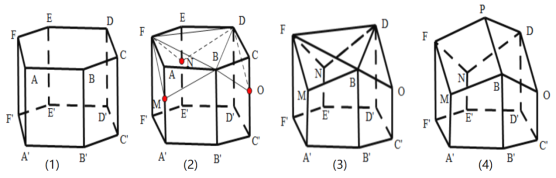
瑞士数学家克尼格利用微积分的方法证明了蜂巢的这种结构是在相同容积下所用材料最省的,英国数学家麦克劳林通过计算得到菱形的一个内角为![]() ,即
,即![]() .以下三个结论①
.以下三个结论①![]() ;②
;② ![]()
![]()
![]() ;③
;③![]() 四点共面,正确命题的个数为______个;若
四点共面,正确命题的个数为______个;若![]() ,
,![]() ,
,![]() ,则此蜂巢的表面积为_______.
,则此蜂巢的表面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》是中国古代重要的数学著作,其记载的“日月历法”曰:“阴阳之数,日月之法,十九岁为一章,四章为一部,部七十六岁,二十部为一遂,遂千百五二十岁,….生数皆终,万物复苏,天以更元作纪历”,某老年公寓住有20位老人,他们的年龄(都为正整数)之和恰好为一遂,其中年长者已是奔百之龄(年龄介于90至100),其余19人的年龄依次相差一岁,则年长者的年龄为( )
A.94B.95C.96D.98
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,2),B为抛物线x2=2y﹣2上任意一点,且B为AC的中点,设动点C的轨迹为曲线E.
(1)求曲线E的方程;
(2)是否存在斜率为1的直线l交曲线E于M、N两点,使得△MAN为以MN为底边的等腰三角形?若存在,请求出l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com