
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,
,![]() 是方程
是方程![]() 的两个不同的实数根,求证:
的两个不同的实数根,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点P为平面上的动点,过点P作直线l:
,点P为平面上的动点,过点P作直线l:![]() 的垂线,垂足为Q,且
的垂线,垂足为Q,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求动点P的轨迹C的方程;
求动点P的轨迹C的方程;
![]() Ⅱ
Ⅱ![]() 设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足
设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村共有100户农民,且都从事蔬菜种植,平均每户的年收入为2万元.为了调整产业结构,该镇政府决定动员部分农民从事蔬菜加工.据估计,若能动员![]() 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高![]() ,而从事蔬菜加工的农民平均每户的年收入为
,而从事蔬菜加工的农民平均每户的年收入为![]() 万元.
万元.
(1)在动员![]() 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的所有棱长都相等,平面BB1C1C⊥平面ABC,BC1=C1C.
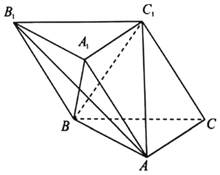
(1)求证:A1B⊥平面AB1C1;
(2)求二面角A1﹣AC1﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的
年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的![]() 次线上测试成绩进行统计如图所示:
次线上测试成绩进行统计如图所示:
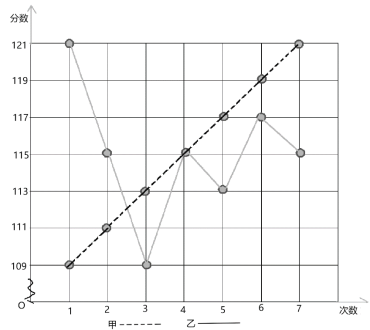
(1)请填写下表(要求写出计算过程)
平均数 | 方差 | |
甲 | ||
乙 |
(2)从下列三个不同的角度对这次方案选择的结果进行
①从平均数和方差相结合看(分析哪种方案的成绩更好);
②从折线图上两种方案的走势看(分析哪种方案更有潜力).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数为( )
(1)![]() 是直线
是直线![]() 和直线
和直线![]() 垂直的充要条件;
垂直的充要条件;
(2)在线性回归方程中,相关系数![]() 越大,变量间的相关性越强;
越大,变量间的相关性越强;
(3)已知随机变量![]() ,若
,若![]() ,则
,则![]()
(4)若命题![]() ,
,![]() ,则
,则![]() ,
,![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界第一产粮大国,我国粮食产量很高,整体很安全按照14亿人口计算,中国人均粮食产量约为950斤﹣比全球人均粮食产量高了约250斤.如图是中国国家统计局网站中2010﹣2019年,我国粮食产量(千万吨)与年末总人口(千万人)的条形图,根据如图可知在2010﹣2019年中( )
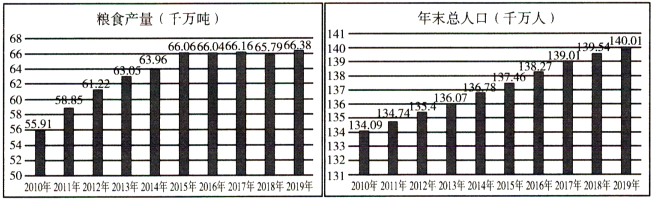
A.我国粮食年产量与年末总人口均逐年递增
B.2011年我国粮食年产量的年增长率最大
C.2015年﹣2019年我国粮食年产量相对稳定
D.2015年我国人均粮食年产量达到了最高峰
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方、堑堵、阳马、鱉臑这些名词出自中国古代数学名著《九章算术商功》.其中阳马和鱉臑是我国古代对一些特殊锥体的称呼.取一长方,如图长方体ABCD﹣A1B1C1D1,按平面ABC1D1斜切一分为二,得到两个一模一样的三棱柱.称该三梭柱为堑堵,再沿堑堵的一顶点与相对的棱剖开,得四棱锥和三棱锥各一个,其中以矩形为底另有一棱与底面垂直的四梭锥D1﹣ABCD称为阳马,余下的三棱锥D1﹣BCC1是由四个直角三角形组成的四面体称为鱉臑.已知长方体ABCD﹣A1B1C1D1中,AB=5,BC=4,AA1=3,按以上操作得到阳马.则该阳马的最长棱长为_____.
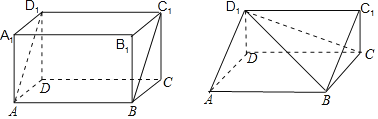
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com