
| A. | 有一个对称中心($\frac{π}{12}$,0) | B. | 有一条对称轴x=$\frac{π}{6}$ | ||
| C. | 在区间[-$\frac{π}{12}$,$\frac{5π}{12}$]上单调递减 | D. | 在区间[-$\frac{π}{12}$,$\frac{5π}{12}$]上单调递增 |
分析 根据最小正周期是π,可得ω,通过变换规律后,图象过点P(0,1),求解φ,可得函数f(x)的解析式,即可判断各选项.
解答 解:由题意,函数f(x)的最小正周期是π,即$\frac{2π}{ω}=π$,∴ω=2.
∴f(x)=sin(2x+φ),
f(x)的图象向左平移$\frac{π}{6}$个单位,可得:sin(2x+$\frac{π}{3}$+φ),此时图象过P(0,1),
可得:$\frac{π}{3}$+φ=$\frac{π}{2}$+2kπ,k∈Z,
∵0<φ<π,
∴φ=$\frac{π}{6}$.
∴f(x)=sin(2x+$\frac{π}{6}$),
令$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$是单调递增,
可得:$-\frac{π}{3}+kπ$$≤x≤\frac{π}{6}+kπ$,k∈Z,
∴C选项不对,
令$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ$是单调递增,
可得:$\frac{π}{6}+kπ$≤x≤$\frac{2π}{3}$+kπ,k∈Z,
∴D选项不对,
由2x+$\frac{π}{6}$=kπ,
得x=$\frac{1}{2}kπ-\frac{π}{12}$
可得对称中心为($\frac{1}{2}kπ-\frac{π}{12}$,0),考查A不对.
由2x+$\frac{π}{6}$=kπ$+\frac{π}{2}$,
得x=$\frac{1}{2}kπ$$+\frac{π}{6}$,
可得对称轴方程为x=$\frac{1}{2}kπ$$+\frac{π}{6}$,
当k=0时,可得x=$\frac{π}{6}$,
∴B选项对.
故选B.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用已知条件求出f(x)解析式是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:填空题
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{3}{10}$ | C. | $-\frac{3}{10}$ | D. | $-\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{16}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{8}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
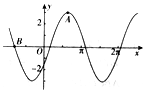 已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).
已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com