
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)求出函数的导数,构造函数h(x),求出函数的导数,得到h(x)的最小值,从而证出结论.
解答 解:(Ⅰ)$f'(x)=\frac{a+1}{x}-\frac{a}{x^2}-1=-\frac{{{x^2}-(a+1)x+a}}{x^2}$=$-\frac{(x-1)(x-a)}{x^2}\;(x>0)$…(2分)
①当a≤0时,令f'(x)>0,得0<x<1;令f'(x)<0,得x>1
则f(x)在(0,1)上递增,在(1,+∞)上递减
②当0<a<1时,令f'(x)>0,得a<x<1;令f'(x)<0,得0<x<a,或x>1
则f(x)在(a,1)上递增,在(0,a)和(1,+∞)上递减
③当a=1时,$f'(x)=-\frac{{{{(x-1)}^2}}}{x^2}≤0$,则f(x)在(0,+∞)上递减
④当a>1时,令f'(x)>0,得1<x<a;令f'(x)<0,得0<x<1,或x>a
则f(x)在(1,a)上递增,在(0,1)和(a,+∞)上递减…(6分)
(Ⅱ)由已知,得$f'(2)=-\frac{2-a}{4}=-\frac{1}{2}$,∴a=0,f(x)=lnx-x…(7分)
令h(x)=g(x)-f(x)=ex-lnx-2(x>0)
则$h'(x)={e^x}-\frac{1}{x}$(x>0)∴h'(x)在(0,+∞)上递增,且$h'(\frac{1}{2})=\sqrt{e}-2<0$,h'(1)=e-1>0,
∴h'(x)有唯一的零点${x_0}∈(\frac{1}{2},1)$,且${e^{x_0}}=\frac{1}{x_0}$,即${e^{-{x_0}}}={x_0}$…(9分)
当x∈(0,x0)时,h'(x)<0,h(x)为减函数
当x∈(x0,+∞)时,h'(x)>0,h(x)为增函数,
∴h(x)min=$h({x_0})={e^{x_0}}-ln{x_0}-2$=$\frac{1}{x_0}-ln{e^{-{x_0}}}-2=\frac{1}{x_0}+{x_0}-2$,
∵${x_0}∈(\frac{1}{2},1)$,∴$\frac{1}{x_0}+{x_0}>2$,∴h(x)min>0,从而h(x)>0,
故对?x∈(0,+∞),f(x)<g(x)…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,-1]∪[7,9) | B. | [-3,-1]∪[7,9) | C. | [7,9) | D. | (-3,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
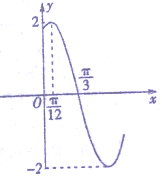 f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间为( )
f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间为( )| A. | [-$\frac{5π}{12}$+kπ,$\frac{π}{12}$+kπ](k∈Z) | B. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{12}$+kπ,$\frac{5π}{12}$+kπ](k∈Z) | D. | [-$\frac{π}{6}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com