练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设全集U＝R，函数f(x)＝lg(|x＋1|＋a－1)(a＜1)的定义域为A，集合B＝{x|cosπx＝1}．若(∁UA)∩B恰好有2个元素，求a的取值集合．


    解：|x＋1|＋a－1＞0|x＋1|＞1－a，

    当a＜1时，1－a＞0，∴ x＞－a或x＜a－2，

    ∴ A＝(－∞，a－2)∪(－a，＋∞)．

    ∵ cosπx＝1，∴ πx＝2kπ，∴ x＝2k(k∈Z)，

    ∴ B＝{x|x＝2k，k∈Z}．

    当a＜1时，∁UA＝[a－2，－a]在此区间上恰有2个偶数．

    ∴.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，在四棱锥P－ABCD中，侧棱PA⊥底面ABCD，底面ABCD为矩形，E为PD上一点，AD＝2AB＝2AP＝2，PE＝2DE.

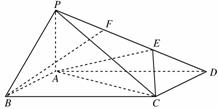
     (1)若F为PE的中点，求证：BF∥平面ACE；

    (2)求三棱锥P－ACE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A＝{y|y＝－2x，x∈[2，3]}，B＝{x|x2＋3x－a2－3a>0}．若AB，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设关于x的不等式x(x－a－1)＜0(a∈R)的解集为M，不等式x2－2x－3≤0的解集为N.

    (1) 当a＝1时，求集合M；

    (2) 若M∪N＝N，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合P＝{(x，y)|x＋y＝0}，Q＝{(x，y)|x－y＝2}，则Q∩P＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列命题中的真命题有________．(填序号)

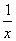    ① x∈R，x＋＝2；

    ② x∈R，sinx＝－1；

    ③ x∈R，x2>0；

    ④ x∈R，2x>0.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若命题改为“存在一个能被2整除的整数是奇数”，其否定为________________________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知向量a＝(x，－1)，b＝(3，y)，其中x随机选自集合{－1,1,3}，y随机选自集合{1,3}，那么a⊥b的概率是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设α，β是两个不同的平面，l是一条直线，以下命题正确的是(　　)

    A．若l⊥α，α⊥β，则l⊂β    B．若l∥α，α∥β，则l⊂β

    C．若l⊥α，α∥β，则l⊥β    D．若l∥α，α⊥β，则l⊥β

    查看答案和解析>>

    同步练习册答案