
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE.
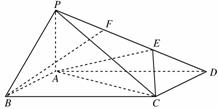
(1)若F为PE的中点,求证:BF∥平面ACE;
(2)求三棱锥P-ACE的体积.
科目:高中数学 来源: 题型:
已知球的半径为5,球面被互相垂直的两个平面所截,得到的两个圆的公共弦长为2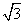 ,若其中一个圆的半径为4,则另一个圆的半径为( )
,若其中一个圆的半径为4,则另一个圆的半径为( )
A.3 B.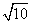
C. D.2
D.2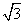
查看答案和解析>>
科目:高中数学 来源: 题型:
“求方程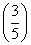 x+
x+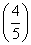 x=1的解”有如下解题思路:设f(x)=
x=1的解”有如下解题思路:设f(x)=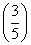 x+
x+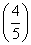 x,则f(x)在R上单调递减,且f(2)=1,所以原方程有唯一解x=2.类比上述解题思路,不等式x6-(x+2)>(x+2)3-x2的解集是________.
x,则f(x)在R上单调递减,且f(2)=1,所以原方程有唯一解x=2.类比上述解题思路,不等式x6-(x+2)>(x+2)3-x2的解集是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有 .
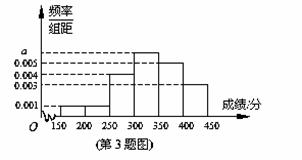
查看答案和解析>>
科目:高中数学 来源: 题型:
设全集U=R,函数f(x)=lg(|x+1|+a-1)(a<1)的定义域为A,集合B={x|cosπx=1}.若(∁UA)∩B恰好有2个元素,求a的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com