练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】正方体的棱长为1，线段上有两个动点 ， 且 ， 则下列结论中错误的是( )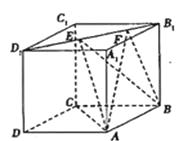

    A.
    B.三棱锥的体积为定值
    C.二面角的大小为定值
    D.异面直线所成角为定值

    【答案】D
    【解析】易知 ， 所以；三棱锥的高就是点到平面的距离且为一定值，为一定值，故三棱锥的体积为定值；二面角的平面角与二面角的平面角相等，故为一定值.
    【考点精析】掌握空间中直线与直线之间的位置关系和直线与平面垂直的判定是解答本题的根本，需要知道相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某市出租车的计价标准是：4km以内（含4km）10元，超过4km且不超过18km的部分1.2元/km，超过18km的部分1.8元/km，不计等待时间的费用．

    （1）如果某人乘车行驶了10km，他要付多少车费？

    （2）试建立车费y（元）与行车里程x（km）的函数关系式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设全集U=R，集合A={x|1≤x＜4}，B={x|2a≤x＜3-a}．

    （1）若a=-2，求B∩A，B∩(UA)；（2）若A∪B=A，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2017·全国卷Ⅲ文，18)某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温(单位：℃)有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20,25)，需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：

    最高气温

    [10,15)

    [15,20)

    [20,25)

    [25,30)

    [30,35)

    [35,40)

    天数

    2

    16

    36

    25

    7

    4

    以最高气温位于各区间的频率估计最高气温位于该区间的概率．

    (1)估计六月份这种酸奶一天的需求量不超过300瓶的概率；

    (2)设六月份一天销售这种酸奶的利润为Y(单位：元)．当六月份这种酸奶一天的进货量为450瓶时，写出Y的所有可能值，并估计Y大于零的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 ， CA=CC1=2CB，则直线BC1与直线AB1夹角的余弦值为（ ）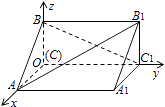

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=logm（m＞0且m≠1），

    （I）判断f（x）的奇偶性并证明；

    （II）若m=，判断f（x）在（3，+∞）的单调性（不用证明）；

    （III）若0＜m＜1，是否存在β＞α>0，使f（x）在[α，β]的值域为[logmm（β-1），logm（α-1）]？若存在，求出此时m的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从装有2只红球，2只白球和1只黑球的袋中逐一取球，已知每只球被抽取的可能性相同.

    (Ⅰ)若抽取后又放回，抽3次.

    (ⅰ)分别求恰2次为红球的概率及抽全三种颜色球的概率；

    (ⅱ)求抽到红球次数的数学期望及方差.

    (Ⅱ)若抽取后不放回，写出抽完红球所需次数的分布列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C，直线（为参数）

    (1)写出曲线C的参数方程和直线l的普通方程;

    (2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=x3﹣3x+2+m（m＞0），在区间[0，2]上存在三个不同的实数a，b，c，使得以f（a），f（b），f（c）为边长的三角形是直角三角形，则m的取值范围是 ．

    查看答案和解析>>

    同步练习册答案