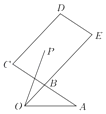
【题目】如图，B是AC的中点，
，P是平行四边形BCDE内（含边界）的一点，且
．有以下结论：
①当x＝0时，y∈[2，3]；
②当P是线段CE的中点时，
；
③若x+y为定值1，则在平面直角坐标系中，点P的轨迹是一条线段；
④x﹣y的最大值为﹣1；
其中你认为正确的所有结论的序号为_____．
科目：高中数学 来源： 题型：
【题目】某小学对五年级的学生进行体质测试，已知五年一班共有学生30人，测试立定跳远的成绩用茎叶图表示如图（单位：
）：男生成绩在175以上（包括175）定义为“合格”，成绩在175以下（不包括175）定义为“不合格”．女生成绩在165以上（包括165）定义为“合格”，成绩在165以下（不包括165）定义为“不合格”．
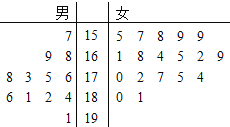
(1)求五年一班的女生立定跳远成绩的中位数；
(2)在五年一班的男生中任意选取3人，求至少有2人的成绩是合格的概率；
(3)若从五年一班成绩“合格”的学生中选取2人参加复试，用
表示其中男生的人数，写出的分布列，并求的数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于实数
，将满足“
且
为整数”的实数
称为实数
的小数部分，用记号
表示．对于实数
，无穷数列
满足如下条件：
，
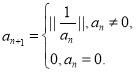其中
．
（1）若
，求数列；
（2）当
时，对任意的
，都有
，求符合要求的实数
构成的集合
；
（3）若
是有理数，设
（
是整数，
是正整数，
互质），问对于大于
的任意正整数
，是否都有
成立，并证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知无穷数列
的前n项和为
，记
， 
，…， 
中奇数的个数为
．
(Ⅰ)若
= n，请写出数列
的前5项；
(Ⅱ)求证："
为奇数， 
(i = 2,3,4,...）为偶数”是“数列
是单调递增数列”的充分不必要条件；
(Ⅲ)若
，i=1, 2, 3,…，求数列
的通项公式.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}是以d为公差的等差数列，{bn}数列是以q为公比的等比数列．
（1）若数列{bn}的前n项和为Sn，且a1＝b1＝d＝2，S3＜a1003+5b2﹣2010，求整数q的值；
（2）在（1）的条件下，试问数列中是否存在一项bk，使得bk恰好可以表示为该数列中连续p（p∈N，p≥2）项的和？请说明理由；
（3）若b1＝ar，b2＝as≠ar，b3＝at（其中t＞s＞r，且（s﹣r）是（t﹣r）的约数），求证：数列{bn}中每一项都是数列{an}中的项．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，以椭圆
（
）的右焦点
为圆心，
为半径作圆（其中
为已知椭圆的半焦距），过椭圆上一点
作此圆的切线，切点为
.
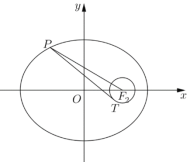
（1）若
，为椭圆的右顶点，求切线长
；
（2）设圆与
轴的右交点为
，过点作斜率为
（
）的直线
与椭圆相交于
、
两点，若
恒成立，且
.求：
（ⅰ）的取值范围；
（ⅱ）直线被圆所截得弦长的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某温室大棚规定，一天中，从中午12点到第二天上午8点为保温时段，其余4小时为工作作业时段，从中午12点连续测量20小时，得出此温室大棚的温度y（单位：度）与时间t（单位：小时，
）近似地满足函数
关系，其中，b为大棚内一天中保温时段的通风量。
（1）若一天中保温时段的通风量保持100个单位不变，求大棚一天中保温时段的最低温度（精确到0.1℃）；
（2）若要保持一天中保温时段的最低温度不小于17℃，求大棚一天中保温时段通风量的最小值。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列1，1，1，2，2，1，2，4，3，1，2，4，8，4，1，2，4，8，16，5，…，其中第一项是
，第二项是1，接着两项为，
，接着下一项是2，接着三项是，，
，接着下一项是3，依此类推.记该数列的前
项和为
，则满足
的最小的正整数的值为（ ）
A.65B.67C.75D.77
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
