
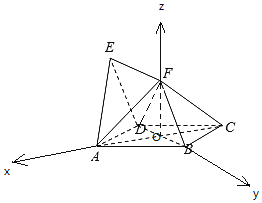
【题目】如图,已知四边形ABCD与四边形BDEF均为菱形,![]() ,且
,且![]()

![]() 求证:
求证:![]() 平面BDEF;
平面BDEF;
![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]() .
.
【解析】
![]() 设AC、BD交于点O,连结OF、DF,推导出
设AC、BD交于点O,连结OF、DF,推导出![]() ,
,![]() ,
,![]() ,由此能证明
,由此能证明![]() 平面BDEF.
平面BDEF.
![]() 以OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出二面角
以OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
![]() 设AC、BD交于点O,连结OF、DF,
设AC、BD交于点O,连结OF、DF,
![]() 四边形ABCD与四边形BDEF均为菱形,
四边形ABCD与四边形BDEF均为菱形,![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 四边形ABCD与四边形BDEF均为菱形,
四边形ABCD与四边形BDEF均为菱形,
![]() ,
,
![]() ,
,![]() 平面BDEF.
平面BDEF.
![]() ,
,![]() ,
,![]() 平面ABCD,
平面ABCD,
![]() 以OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,
以OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,
设![]() ,则
,则![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
![]() ,
,![]() 1,
1,![]() ,
,
![]() ,
,
设平面ABF的法向量![]() y,
y,![]() ,
,
则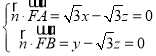 ,取
,取![]() ,得
,得![]() ,
,
设平面BCF的法向量![]() y,
y,![]() ,
,
则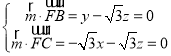 ,取
,取![]() ,得
,得![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,由图可知为钝角
,由图可知为钝角
则![]() .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为4 800立方米,深度为3米.池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底长方形长为x米.
(1)求底面积,并用含x的表达式表示池壁面积;
(2)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难题的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度,![]() 为答对该题的人数,
为答对该题的人数,![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
学生 编号 题号 | 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;
题号 | 1 | 2 | 3 | 4 | 5 |
实测答对人数 | |||||
实测难度 |
(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度,![]() 为第
为第![]() 题的预估难度(
题的预估难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某市2015年全年空气质量等级如表1所示.
表1
空气质量等级(空气质量指数(AQI)) | 频数 | 频率 |
优( | 83 | 22.8% |
良( | 121 | 33.2% |
轻度污染( | 68 | 18.6% |
中度污染( | 49 | 13.4% |
重度污染( | 30 | 8.2% |
严重污染( | 14 | 3.8% |
合计 | 365 | 100% |
2016年5月和6月的空气质量指数如下:
5月 240 80 56 53 92 126 45 87 56 60
191 62 55 58 56 53 89 90 125 124
103 81 89 44 34 53 79 81 62 116
88
6月 63 92 110 122 102 116 81 163 158 76
33 102 65 53 38 55 52 76 99 127
选择合适的统计图描述数据,并回答下列问题:
(1)分析该市2016年6月的空气质量情况.
(2)比较该市2016年5月和6月的空气质量,哪个月的空气质量较好?
(3)比较该市2016年6月与该市2015年全年的空气质量,2016年6月的空气质量是否好于去年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)如果函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)若不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是我国某城市在2017年1月份至10月份各月最低温与最高温![]() 的数据一览表
的数据一览表

已知该城市的各月最低温与最高温具有线性相关关系,根据该一览表,则下列结论错误的是 ( )
A. 最低温与最高温为正相关
B. 每月最高温与最低温的平均值前8个月逐月增加
C. 月温差(最高温减最低温)的最大值出现在1月
D. 1月至4月的月温差(最高温减最低温)相对于7月至10月,波动性更大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的首项
的首项![]() ,前
,前![]() 项和
项和![]() 满足关系式
满足关系式![]() .
.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)设数列![]() 的公比为
的公比为![]() ,作数列
,作数列![]() ,使
,使![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)数列![]() 满足条件(2),求和:
满足条件(2),求和:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com