练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

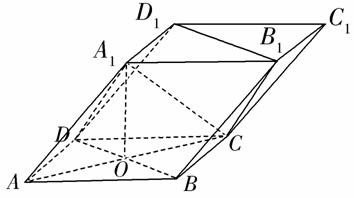
    如图，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥底面ABCD，AB＝AA1＝.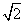

    (1)证明：平面A1BD∥平面CD1B1；

    (2)求三棱柱ABD－A1B1D1的体积．


    [解析]　(1)由题设知，BB1綊DD1，

    ∴BB1D1D是平行四边形，

    ∴BD∥B1D1.

    又BD平面CD1B1，

    ∴BD∥平面CD1B1.

    ∵A1D1綊B1C1綊BC，

    ∴A1BCD1是平行四边形，

    ∴A1B∥D1C.又A1B平面CD1B1，

    ∴A1B∥平面CD1B1.

    又∵BD∩A1B＝B，

    ∴平面A1BD∥平面CD1B1.

    (2)∵A1O⊥平面ABCD，

    ∴A1O是三棱柱ABD－A1B1D1的高．

    又∵AO＝AC＝1，AA1＝，

    ∴A1O＝＝1.

    又∵S△ABD＝××＝1，

    ∴V三棱柱ABD－A1B1D1＝S△ABD×A1O＝1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


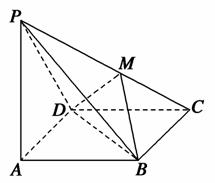
    如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足______时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b为两条不同的直线，α，β为两个不同的平面，且a⊥α，b⊥β，则下列命题中的假命题是(　　)

    A．若a∥b，则α∥β

    B．若α⊥β，则a⊥b

    C．若a，b相交，则α，β相交

    D．若α，β相交，则a，b相交

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在四棱锥P－ABCD中，底面ABCD是矩形，已知AB＝3，AD＝2，PA＝2，PD＝2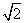，∠PAB＝60°.M是PD的中点．

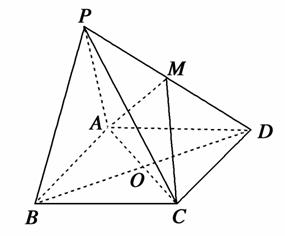
    (1)证明：PB∥平面MAC；

    (2)证明：平面PAB⊥平面ABCD；

    (3)求四棱锥P－ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设m，n是平面α内的两条不同直线；l1，l2是平面β内的两条相交直线，则α∥β的一个充分而不必要条件是(　　)

    A．m∥β且l1∥α　　　　　B．m∥l1且n∥l2

    C．m∥β且n∥β  D．m∥β且n∥l2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，c为三条不重合的直线，α，β，γ为三个不重合的平面，直线均不在平面内，给出六个命题：

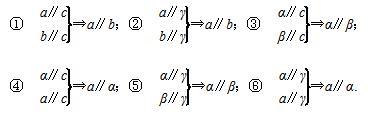    其中正确的命题是________(将正确命题的序号都填上)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面α垂直于平面β(α、β为不重合的平面)成立的一个充分条件是(　　)

    A．存在一条直线l，l⊥α，l⊥β

    B．存在一个平面γ，γ∥α，γ∥β

    C．存在一个平面γ，γ⊥α，γ⊥β

    D．存在一条直线l，l⊥α，l∥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个与球心距离为1的平面截球所得的圆面面积为π，则球的表面积为(　　)

    A．8π　　　　　　　　　                       B．8π

    C．4π　　　                                           D．4π

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在空间四边形ABCD中，＝________.

    查看答案和解析>>

    同步练习册答案