
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2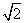 ,∠PAB=60°.M是PD的中点.
,∠PAB=60°.M是PD的中点.
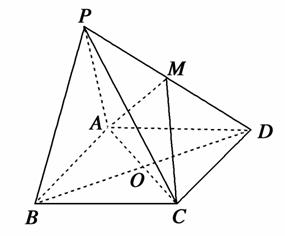
(1)证明:PB∥平面MAC;
(2)证明:平面PAB⊥平面ABCD;
(3)求四棱锥P-ABCD的体积.
[解析] (1)证明:连接OM.
∵M是PD中点,矩形ABCD中O为BD中点,
∴OM∥PB.
又OM平面MAC,PB⃘平面MAC,
∴PB∥平面MAC.
(2)证明:由题设知PA=2,AD=2,PD=2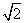 ,
,
有PA2+AD2=PD2,∴AD⊥PA.
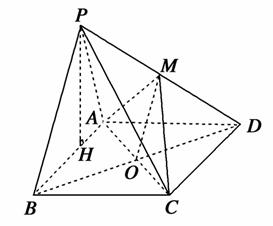
在矩形ABCD中,AD⊥AB.
又PA∩AB=A,∴AD⊥平面PAB.
∵AD平面ABCD,
∴平面PAB⊥平面ABCD.
(3)解:过点P作PH⊥AB于点H.
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
∴PH⊥平面ABCD.
在Rt△PHA中,PH=PAsin60°=2×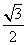 =
=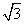 ,
,
VP-ABCD=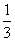 AB×AD×PH=
AB×AD×PH=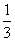 ×3×2×
×3×2×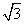 =2
=2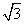 .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
如图,正方体ABCD-A1B1C1D1中,E、F分别为棱AB、CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线( )
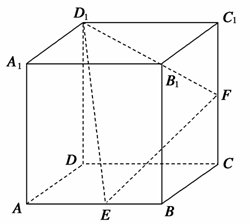
A.不存在 B.有1条
C.有2条 D.有无数条
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a,b为不垂直的异面直线,α是一个平面,则a,b在α上的射影有可能是:
①两条平行直线;
②两条互相垂直的直线;
③同一条直线;
④一条直线及其外一点.
在上面结论中,正确结论的编号是________(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( )
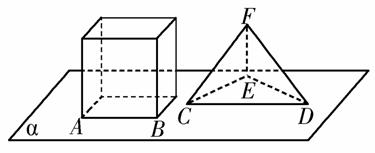
A.8 B.9
C.10 D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,P为平行四边形ABCD所在平面外的一点,过BC的平面与平面PAD交于EF,则四边形EFBC是( )
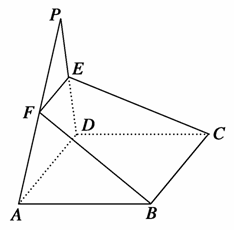
A.空间四边形 B.平行四边形
C.梯形 D.以上都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥底面ABCD,AB=AA1=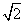 .
.
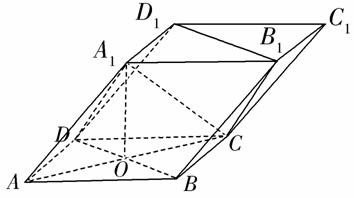
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题中错误的是( )
A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ
D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com