练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，P为平行四边形ABCD所在平面外的一点，过BC的平面与平面PAD交于EF，则四边形EFBC是(　　)

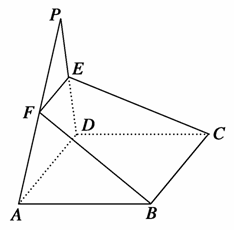
    A．空间四边形　　　　　                             B．平行四边形

    C．梯形                                                        D．以上都有可能


    　C

    [解析]　∵BC綊AD，由线面平行性质定理知BC∥EF，

    又EF<AD，∴四边形BCEF为梯形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


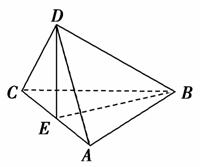
     如图，在立体图形D－ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列结论正确的是(　　)

    A．平面ABC⊥平面ABD

    B．平面ABD⊥平面BDC

    C．平面ABC⊥平面BDE，且平面ADC⊥平面BDE

    D．平面ABC⊥平面ADC，且平面ADC⊥平面BDE

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a、b是异面直线，直线c∥直线a，则c与b(　　)

    A．一定是异面直线                                       B．一定是相交直线

    C．不可能是平行直线                                   D．不可能是相交直线

    查看答案和解析>>

    科目：高中数学 来源： 题型：


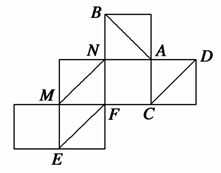
    一个正方体纸盒展开后如图，在原正方体纸盒中有下列结论：

    ①AB⊥EF；②AB与CM成60°的角；③EF与MN是异面直线；④MN∥CD.其中正确的是(　　)

    A．①②                                                        B．③④

    C．②③                                                        D．①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在四棱锥P－ABCD中，底面ABCD是矩形，已知AB＝3，AD＝2，PA＝2，PD＝2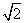，∠PAB＝60°.M是PD的中点．

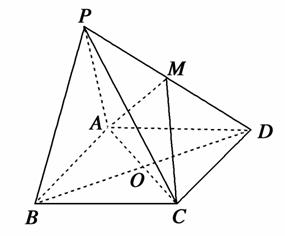
    (1)证明：PB∥平面MAC；

    (2)证明：平面PAB⊥平面ABCD；

    (3)求四棱锥P－ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过三棱柱ABC－A1B1C1的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有________条．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，c为三条不重合的直线，α，β，γ为三个不重合的平面，直线均不在平面内，给出六个命题：

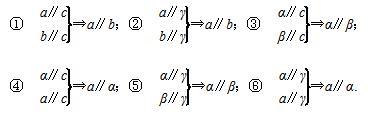    其中正确的命题是________(将正确命题的序号都填上)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，直四棱柱ABCD－A1B1C1D1中，AB//CD，AD⊥AB，AB＝2，AD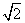＝，AA1＝3，E为CD上一点，DE＝1，EC＝3.

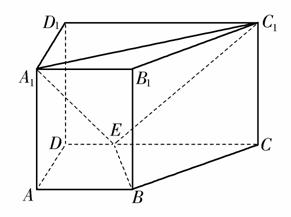
    (1)证明：BE⊥平面BB1C1C；

    (2)求点B1 到平面EA1C1 的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，在棱长为2的正方体OABC－O1A1B1C1的对角线O1B上有一点P，棱B1C1上有一点Q.

    (1)当Q为B1C1的中点，点P在对角线O1B上运动时，试求|PQ|的最小值；

    (2)当Q在B1C1上运动，点P在O1B上运动时，试求|PQ|的最小值．

    查看答案和解析>>

    同步练习册答案