
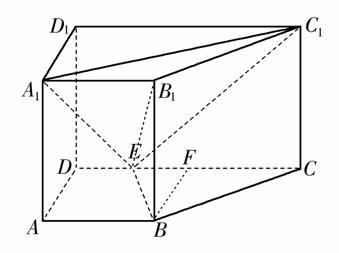
如图,直四棱柱ABCD-A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=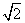 ,AA1=3,E为CD上一点,DE=1,EC=3.
,AA1=3,E为CD上一点,DE=1,EC=3.
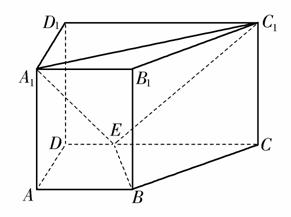
(1)证明:BE⊥平面BB1C1C;
(2)求点B1 到平面EA1C1 的距离.
[解析] (1)证明:过B作CD的垂线交CD于F,则
BF=AD=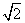 ,EF=AB-DE=1,FC=2.
,EF=AB-DE=1,FC=2.
在Rt△BFE中,BE=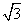 .
.
在Rt△CFB中,BC=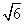 .
.
在△BEC中,因为BE2+BC2=9=EC2,故BE⊥BC.
由BB1⊥平面ABCD得BE⊥BB1,
所以BE⊥平面BB1C1C.
(2)连接B1E,则三棱锥E-A1B1C1的体积V=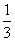 AA1·S△A1B1C1=
AA1·S△A1B1C1=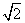 .
.
在Rt△A1D1C1中,A1C1=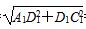 =3
=3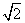 .
.
同理,EC1=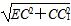 =3
=3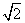 .
.
A1E=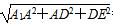 =2
=2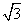 ,
,
故S△A1C1E=3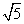 .
.
设点B1到平面EA1C1的距离为d,
则三棱锥B1-A1C1E的体积
V=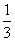 ·d·S△A1C1E=
·d·S△A1C1E=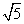 d,
d,
从而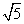 d=
d=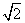 ,d=
,d=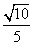 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
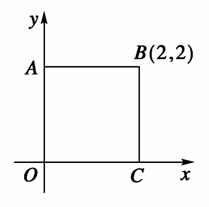
上图为水平放置的正方形ABCO,它在直角坐标系xOy中点B的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为( )
A.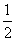 B.
B.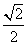
C.1 D.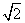
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,P为平行四边形ABCD所在平面外的一点,过BC的平面与平面PAD交于EF,则四边形EFBC是( )
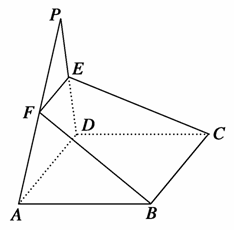
A.空间四边形 B.平行四边形
C.梯形 D.以上都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
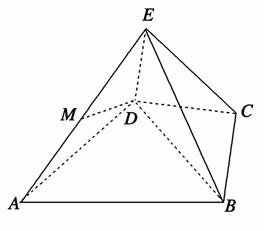
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题中错误的是( )
A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ
D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
查看答案和解析>>
科目:高中数学 来源: 题型:
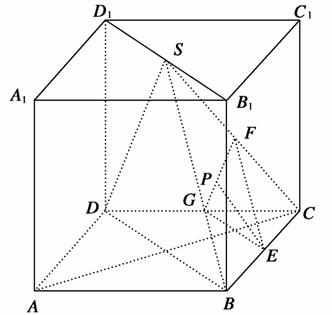
在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、SC和DC的中点,点P在线段FG上.
(1)求证:平面EFG∥平面SDB;
(2)求证:PE⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
在空间直角坐标系中,已知点P(x,y,z),给出下列四条叙述:
①点P关于x轴的对称点的坐标是(x,-y,z);
②点P关于yOz平面的对称点的坐标是(x,-y,-z);
③点P关于y轴的对称点的坐标是(x,-y,z);
④点P关于原点的对称点的坐标是(-x,-y,-z).
其中正确的个数是( )
A.3 B.2
C.1 D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
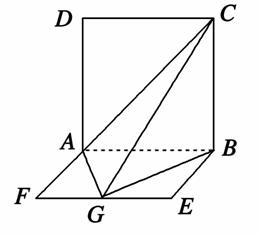
如图,平面ABCD⊥平面ABEF,四边ABCD是正方形,四边形ABEF是矩形,且AF=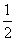 AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为________.
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com