练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

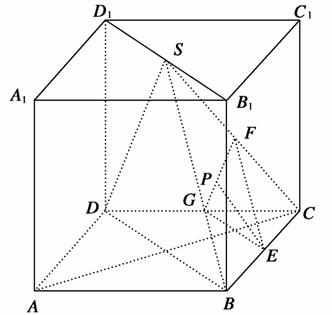
    在正方体ABCD－A1B1C1D1中，S是B1D1的中点，E、F、G分别是BC、SC和DC的中点，点P在线段FG上．

    (1)求证：平面EFG∥平面SDB；

    (2)求证：PE⊥AC.


    [解析]　(1)∵E、F、G分别为BC、SC、CD的中点，

    ∴EF∥SB，EG∥BD.

    ∵EF平面SBD，EG平面SBD，

    ∴EF∥平面SBD，EG∥平面SBD.

    ∵EG∩EF＝E，∴平面EFG∥平面SDB.

    (2)∵B1B⊥底面ABCD，∴AC⊥B1B.

    又∵四边形ABCD是正方形，∴AC⊥BD.

    ∴AC⊥平面B1BDD1，即AC⊥平面SBD.

    又平面EFG∥平面SBD，∴AC⊥平面EFG.

    ∵PE平面EFG，∴PE⊥AC.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如下的三个图中，上面是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出(单位：cm)．

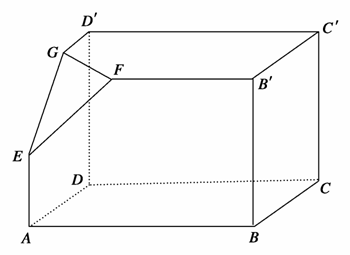
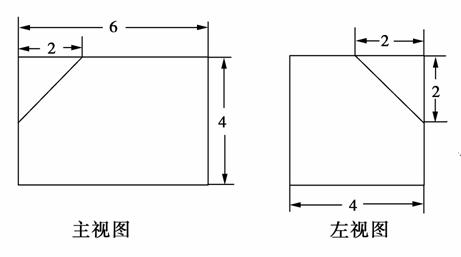
    (1)在主视图下面，按照画三视图的要求画出该多面体的俯视图；

    (2)按照给出的尺寸，求该多面体的体积

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过三棱柱ABC－A1B1C1的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有________条．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设l是直线，α，β是两个不同的平面(　　)

    A．若l∥α，l∥β，则α∥β                            B．若l∥α，l⊥β，则α⊥β

    C．若α⊥β，l⊥α，则l⊥β                            D．若α⊥β，l∥α，则l⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，直四棱柱ABCD－A1B1C1D1中，AB//CD，AD⊥AB，AB＝2，AD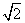＝，AA1＝3，E为CD上一点，DE＝1，EC＝3.

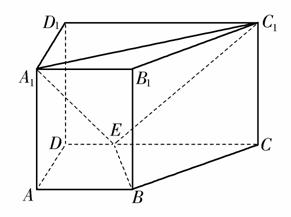
    (1)证明：BE⊥平面BB1C1C；

    (2)求点B1 到平面EA1C1 的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为(　　)

    A.π                                                         B．4π

    C．4π                                                     D．6π

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体的三视图如图所示，则其表面积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知A(3,5，－7)和点B(－2,4,3)，则线段AB在坐标平面yOz上的射影的长度为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    光线自点M(2,3)射到N(1,0)后被x轴反射，则反射光线所在的直线方程为(　　)

    A．y＝3x－3                                                 B．y＝－3x＋3

    C．y＝－3x－3                                              D．y＝3x＋3

    查看答案和解析>>

    同步练习册答案