
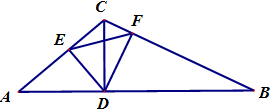
分析 (1)证明:∠A+∠EFB=180°,即可证明A,E,F,B四点共圆;
(2)由△CEF~△ACB得$\frac{EF}{AB}$的值.
解答  (1)证明:∵CD⊥AB,DE⊥AC,∴∠A=∠CDE,
(1)证明:∵CD⊥AB,DE⊥AC,∴∠A=∠CDE,
又∵DF⊥BC,∴∠CED=∠CFD=90°,则C、E、D、F四点共圆,
所以∠CDE=∠CFE,∴∠A=∠CFE,
故∠A+∠EFB=180°,A、E、F、B四点共圆;
(2)解:由△CEF~△ACB得,$\frac{EF}{AB}=\frac{CE}{BC}=\frac{{\frac{{\sqrt{2}}}{2}CD}}{2CD}=\frac{{\sqrt{2}}}{4}$.
点评 本题考查四点共圆的证明,考查三角形相似性质的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}π$ | B. | $\frac{{\sqrt{3}}}{2}π$ | C. | $\frac{{5\sqrt{5}}}{6}π$ | D. | $\sqrt{6}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
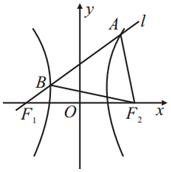 如图,F1、F2分别为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点,过F1的直线l交C于A、B两点,若C的离心率为$\sqrt{7}$,|AB|=|AF2|,则直线l的斜率为( )
如图,F1、F2分别为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点,过F1的直线l交C于A、B两点,若C的离心率为$\sqrt{7}$,|AB|=|AF2|,则直线l的斜率为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 观察图中各正方形图案,每条边上有an个圆点,第an个图案中圆点的个数是an,按此规律推断出所有圆点总和Sn与n的关系式为( )
观察图中各正方形图案,每条边上有an个圆点,第an个图案中圆点的个数是an,按此规律推断出所有圆点总和Sn与n的关系式为( )| A. | ${S_n}=2{n^2}-2n$ | B. | ${S_n}=2{n^2}$ | C. | ${S_n}=4{n^2}-3n$ | D. | ${S_n}=2{n^2}+2n$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com