
【题目】某地拟规划种植一批芍药,为了美观,将种植区域(区域I)设计成半径为1km的扇形![]() ,中心角
,中心角![]() (
(![]() ).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形
).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形![]() ,其中点
,其中点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
(1)要使观赏区的年收入不低于5万元,求![]() 的最大值;
的最大值;
(2)试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?

 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上且
上且![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
在棱![]() 上且
上且![]() ,点
,点![]() 位棱
位棱![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值的大小.
的余弦值的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线M上的动点![]() 到定点
到定点![]() 距离是它到定直线
距离是它到定直线![]() 距离的一半.
距离的一半.
(1)求曲线M的方程;
(2)设过点![]() 且倾斜角为
且倾斜角为![]() 的直线与曲线M相交与A、B两点,在定直线l上是否存在点C,使得
的直线与曲线M相交与A、B两点,在定直线l上是否存在点C,使得![]() ,若存在,求出点C的坐标,若不存在,请说明理由.
,若存在,求出点C的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,(
,(![]() )其图象上任意一点
)其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() ,方程
,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为![]() 万元,每生产
万元,每生产![]() 千件需另投入
千件需另投入![]() 万元.设该公司一年内共生产该品牌服装
万元.设该公司一年内共生产该品牌服装![]() 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且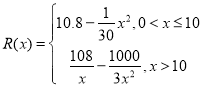 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入-年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为调查该校学生每周参加社会实践活动的情况,随机收集了若干名学生每周参加社会实践活动的时间(单位:小时),将样本数据绘制如图所示的频率分布直方图,且在[0,2)内的学生有1人.
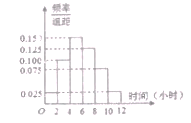
(1)求样本容量![]() ,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
(2)将每周参加社会实践活动时间在[4,12]内定义为“经常参加社会实践”,参加活动时间在[0,4)内定义为“不经常参加社会实践”.已知样本中所有学生都参加了青少年科技创新大赛,有13人成绩等级为“优秀”,其余成绩为“一般”,其中成绩优秀的13人种“经常参加社会实践活动”的有12人.请将2×2列联表补充完整,并判断能否在犯错误的概率不超过0.05的前提下认为青少年科技创新大赛成绩“优秀”与经常参加社会实践活动有关;
(3)在(2)的条件下,如果从样本中“不经常参加社会实践”的学生中随机选取两人参加学校的科技创新班,求其中恰好一人成绩优秀的概率.
参考公式和数据:
![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)若出现故障的机器台数为![]() ,求
,求![]() 的分布列;
的分布列;
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com