
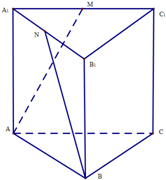
 正三棱柱A1B1C1-ABC,$AC=2,C{C_1}=\sqrt{2}$,M,N为A1C1,A1B1的中点,则异面直线AM与BN所成角( )
正三棱柱A1B1C1-ABC,$AC=2,C{C_1}=\sqrt{2}$,M,N为A1C1,A1B1的中点,则异面直线AM与BN所成角( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 以A为原点,在平面ABC内过A作AC的垂线为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AM与BN所成角.
解答 解:以A为原点,在平面ABC内过A作AC的垂线为x轴,AC为y轴,AA1为z轴,
建立空间直角坐标系,
A(0,0,0),M(0,1,$\sqrt{2}$),B($\sqrt{3}$,1,0),N($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,$\sqrt{2}$),
$\overrightarrow{AM}$=(0,1,$\sqrt{2}$),$\overrightarrow{BN}$=(-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,$\sqrt{2}$),
设异面直线AM与BN所成角为θ,
则cosθ=$\frac{|\overrightarrow{AM}•\overrightarrow{BN}|}{|\overrightarrow{AM}|•|\overrightarrow{BN}|}$=$\frac{\frac{3}{2}}{\sqrt{3}•\sqrt{3}}$=$\frac{1}{2}$,
∴$θ=\frac{π}{3}$,
∴异面直线AM与BN所成角为$\frac{π}{3}$.
故选:C.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 126 | B. | 63 | C. | 64 | D. | 127 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某种产品的广告费用支出x万元与销售额y万元之间有如图的对应数据:
某种产品的广告费用支出x万元与销售额y万元之间有如图的对应数据:| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 30 | 50 | 50 | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com