0.1.1.2.2.2.2七个数字全取排成七位数.有90种方法．题目和参考答案——青夏教育精英家教网—

17．0、1、1、2、2、2、2七个数字全取排成七位数，有90种方法．

分析不考虑首位是0，有$\frac{{A}_{7}^{7}}{{A}_{2}^{2}{A}_{4}^{4}}$=105种方法；首位是0，有$\frac{{A}_{6}^{6}}{{A}_{2}^{2}{A}_{4}^{4}}$=15种方法，即可得出结论．

解答解：不考虑首位是0，有$\frac{{A}_{7}^{7}}{{A}_{2}^{2}{A}_{4}^{4}}$=105种方法；首位是0，有$\frac{{A}_{6}^{6}}{{A}_{2}^{2}{A}_{4}^{4}}$=15种方法，
∴共有105-15=90种方法．
故答案为：90．

点评本题考查排列知识的运用，考查学生的计算能力，比较基础．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

7．已知直线（3a+2）x+（1-4a）y+8=0与（5a-2）x+（a+4）y-7=0垂直，则实数a=（　　）

A．

B．

C．

0或1

D．

0或-1

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．在标准化的考试中既有单选题又有多选题，多选题是从A，B，C，D四个选项中选出所有正确的答案（正确答案可能是一个或多个选项），有一道多选题考生不会做，若他随机作答，则他答对的概率是（　　）

A．

$\frac{1}{4}$

B．

$\frac{1}{12}$

C．

$\frac{1}{15}$

D．

$\frac{1}{16}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．

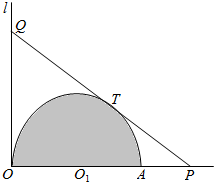如图，阴影部分为古建筑物保护群所在地，其形状是以O₁为圆心，半径为1km的半圆面．公路l经过点O，且与直径OA垂直，现计划修建一条与半圆相切的公路PQ（点P在直径OA的延长线上，点Q在公路l上），T为切点．
（1）按下列要求建立函数关系：
①设∠OPQ=α（rad），将△OPQ的面积S表示为α的函数；
②设OQ=t（km），将△OPQ的面积S表示为t的函数．
（2）请你选用（1）中的一个函数关系，求△OPQ的面积S的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

12．若1og_a$\frac{2}{3}$＜0，则实数a的取值范围是（　　）

A．

（$\frac{2}{3}$，1）

B．

（$\frac{2}{3}$，+∞）

C．

（0，1）

D．

（1，+∞）

查看答案和解析>>