
分析 由题意得,函数f(x)在原点处于x轴相切,即导函数在x=0处等于0,同时可令导函数为0,解得两个极值,其中有一个为-$\frac{4}{27}$
解答 ∵f(x)与直线y=0在原点处相切
f′(x)=3x2+2ax+b
∴$f′(0)=0\\;\\;∴b=0$
∴f(x)=x3+ax2
f′(x)=3x2+2ax
=x(3x+2a)
令f′(x)=0,则x1=0,${x}_{2}=-\frac{2a}{3}$
∵f(0)=0
$f(-\frac{2a}{3})=\frac{4}{27}{a}^{3}$
∴$\frac{4}{27}{a}^{3}=-\frac{4}{27}$
∴a3=-1
∴a=-1
故答案为a=-1
点评 本题以函数为载体,考查函数的极值及在某点处的相切.属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
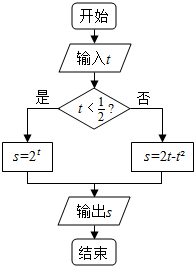
| A. | [0,1] | B. | [$\frac{3}{4}$,$\sqrt{2}$] | C. | [0,$\sqrt{2}$] | D. | [1,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
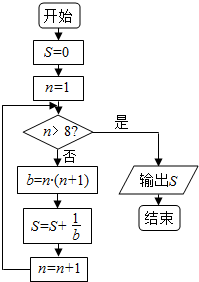
| A. | $\frac{7}{8}$ | B. | $\frac{9}{10}$ | C. | $\frac{8}{9}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
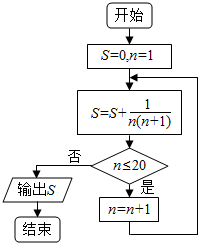
| A. | $\frac{19}{20}$ | B. | $\frac{20}{21}$ | C. | $\frac{21}{22}$ | D. | $\frac{22}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com