
分析 (1)分x<-2,-2≤x≤2,x>2三种情况去绝对值符号将不等式转化为一元一次不等式求解;
(2)分别求出a+b和x$+\frac{4}{x}$+m的范围,令a+b的最大值小于x$+\frac{4}{x}$+m的最小值即可.
解答 解:(1)①当x<-2时,-x-2-x+2<18,解得-9<x<-2;
②当-2≤x≤2时,x+2-x+2<18,恒成立;
③当x>2时,x+2+x-2<18,解得2<x<9.
综上,不等式|x+2|+|x-2|<18的解集为(-9,-2)∪[-2,2]∪(2,9)=(-9,9).
∴A=(-9,9).
(2)∵a,b∈(-9,9),∴a+b∈(-18,18).∵a+b<x$+\frac{4}{x}$+m恒成立,
∴18≤x$+\frac{4}{x}$+m恒成立,∵x∈(0,+∞),∴x+$\frac{4}{x}$+m≥2$\sqrt{x•\frac{4}{x}}$+m=4+m.
∴18≤4+m,解得m≥14.
∴m的取值范围是[14,+∞).
点评 本题考查了绝对值不等式的解法,基本不等式的性质,函数恒成立问题,属于中档题.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/份 | 440 | 400 | 360 | 320 | 280 | 240 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.43<30.4<log43 | B. | log43<0.43<30.4 | C. | 0.43<log43<30.4 | D. | log43<30.4<0.43 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
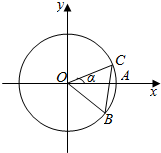 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | -$\frac{5}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com