
| A. | $({1,\sqrt{2}})$ | B. | $({1,\sqrt{2}+1}]$ | C. | $({\sqrt{2},\sqrt{2}+1}]$ | D. | $[{\sqrt{2}+1,+∞})$ |
分析 由双曲线的定义可得 PF′-PF=2a,以及双曲线的第二定义得PF=$\frac{2a}{e-1}$=$\frac{2{a}^{2}}{c-a}$≥c-a,建立a,c的关系进行求解即可.
解答 解:设双曲线的右焦点F (c,0),左焦点F′(-c,0 ),
由双曲线的定义可得 PF′-PF=2a,以及圆锥曲线的第二定义得 $\frac{PF′}{PF}$=e,
∴ePF-PF=2a,
∴PF=$\frac{2a}{e-1}$=$\frac{2{a}^{2}}{c-a}$≥c-a,
∴$\frac{c}{a}$≤$\sqrt{2}$+1.
再由 e>1,∴1<e≤$\sqrt{2}$+1,
故选 B.
点评 本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,利用双曲线的第二定义是解决本题的关键.综合性较强.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
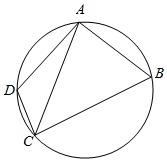 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com