练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知直线：，直线：，其中，．
    （1）求直线的概率；
    （2）求直线与的交点位于第一象限的概率．
    （1）（2）
    （1）解：直线的斜率，直线的斜率．
    设事件为“直线”．
    ，的总事件数为，，…，，，，…，，…，，共36种．
    若，则，即，即．
    满足条件的实数对有、、共三种情形．
    所以．
    答：直线的概率为．
    （2）解：设事件为“直线与的交点位于第一象限”，由于直线与有交点，则．
    联立方程组解得 
    因为直线与的交点位于第一象限，则 
    即解得．
    ，的总事件数为，，…，，，，…，，…，，共36种．
    满足条件的实数对有、、、、、共六种．
    所以．
    答：直线与的交点位于第一象限的概率为．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    在一次体操选拔赛中，教练组设置了难度不同的甲、乙两个系列，每个系列都有A和B两个动作．比赛时每位运动员自选一个系列完成，两个动作得分之和为该运动员的成绩．
    假设每个运动员完成每个系列中的两个动作的得分是相互独立的．根据赛前训练统计数据，某运动员完成甲系列和乙系列的情况如下表：
    表1：甲系列           表2：乙系列

    动作

    		A动作
    		B动作
    得分
    		100
    		80
    		40
    		10
    概率




     
     
    动作
    		A动作
    		B动作
    得分
    		90
    		50
    		20
    		0
    概率




     
     
     

     
    现该运动员最后一个出场，之前其他运动员的最高得分为115分．
    （Ⅰ）若该运动员希望获得该项目的第一名，应选择哪个系列？说明理由，并求其获得第一名的概率；
    （Ⅱ）若该运动员选择乙系列，求其成绩的分布列及其数学期望．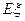

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

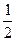    甲乙丙三人参加一家公司的招聘面试，面试合格者可正式签约。甲表示只要面试合格就签约，乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约。设每人面试合格的概率都是，且面试是否合格互不影响。求：
    （I）至少一人面试合格的概率；
    （II）没有人签约的概率。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    在一次食品卫生大检查中，执法人员从抽样中得知，目前投放我市的甲、乙两种食品的合格率分别为和。
    （１）今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率.
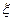    （2）若某消费者从两种食品中任意各购一件,设表示购得不合格食品的件数,试写出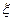的分布列,并求其数学期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    甲、乙两人进行射击比赛，在一轮比赛中，甲、乙各射击一发子弹。根据以往资料知，甲击中8环，9环，10环的概率分别为0.6，0.3，0.1，乙击中8环，9环，10环的概率分别为0.4，0.4，0.2。
    设甲、乙的射击相互独立。
    （Ⅰ）求在一轮比赛中甲击中的环数多于乙击中环数的概率；
    （Ⅱ）求在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数的概率。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    森林公园有甲、乙两个相邻景点，原拟定甲景点内有2个A班的同学和2个B班的同学；乙景点内有2个A班同学和3个B班同学，后由于某种原因甲乙两景点各有一个同学交换景点观光.
    （1）求甲景点恰有2个A班同学的概率；
    （2）求甲景点A班同学数ξ的分布列及期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某电视台“挑战主持人”节目的挑战者闯第一关需要回答3个问题，其中前两个问
    题回答正确各得10分，回答不正确各得0分，第三题回答正确得20分，回答不正确得-10分，总得分不少于30分即可过关．如果一位挑战者回答前两题正确的概率都是，回答第三题正确的概率为，且各题回答正确与否相互之间没有影响．记这位挑战者回答这三个问题的总得分为。
    （1）求这位挑战者过关的概率有多大；  （2）求的概率分布和数学期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

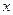    调查某市出租车使用年限和该年支出维修费用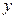（万元），得到数据如下：
    使用年限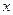
    		2
    		3
    		4
    		5
    		6
    维修费用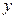
    		2．2
    		3．8
    		5．5
    		6．5
    		7．0
    （1）      求线性回归方程；
    （2）由（1）中结论预测第10年所支出的维修费用．（）

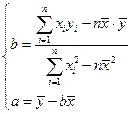    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    从0，1，2，3，4，5六个数字中，任取五个不同的数字组成一个五位数，则该数能被2或5整除的概率为__________

    查看答案和解析>>

    同步练习册答案