Question

17．已知抛物线y²=2px（p＞0）的准线与x轴交于点N，过点N作圆M：（x-2）²+y²=1的两条切线，切点为P、Q，且|PQ|=$\frac{4\sqrt{2}}{3}$．
（1）求抛物线的方程；
（2）过抛物线的焦点F作斜率为k₁的直线与抛物线交于A、B两点，A、B两点的横坐标均不为2，连接AM，BM并延长分别交抛物线于C、D两点，设直线CD的斜率为k₂，问$\frac{{k}_{1}}{{k}_{2}}$是否为定值？若是，求出该定值；若不是，说明理由．

Answer 1

分析 （1）求得抛物线的准线方程，可得N的坐标，圆M的圆心和半径，可得四点N，P，M，Q共圆，且MN为直径，设为2R，在△PMQ中，运用余弦定理和正弦定理，可得2R=3，求得p=2，即可得到抛物线的方程；
（2）求得抛物线y²=4x的焦点为F（1，0），设A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），D（x₄，y₄），运用直线的斜率公式，求得k₁，k₂，及$\frac{{k}_{1}}{{k}_{2}}$，设出直线AC，BD和AB的方程，联立抛物线的方程，运用韦达定理，计算即可得到定值2．

解答 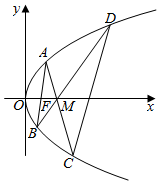解：（1）抛物线y²=2px（p＞0）的准线为x=-$\frac{p}{2}$，N（-$\frac{p}{2}$，0），
圆M：（x-2）²+y²=1的圆心M（2，0），半径r=1，
由PM⊥PN，QM⊥QN，可得四点N，P，M，Q共圆，且MN为直径，设为2R，
在△PMQ中，|MP|=|MQ|=1，|PQ|=$\frac{4\sqrt{2}}{3}$，
由余弦定理可得cos∠PMQ=$\frac{1+1-\frac{32}{9}}{2×1×1}$=-$\frac{7}{9}$，
可得sin∠PMQ=$\sqrt{1-\frac{49}{81}}$=$\frac{4\sqrt{2}}{9}$，
即有2R=$\frac{|PQ|}{sin∠PMQ}$=$\frac{4\sqrt{2}}{3}$×$\frac{9}{4\sqrt{2}}$=3，
即2+$\frac{p}{2}$=3，解得p=2，
可得抛物线的方程为y²=4x；
（2）抛物线y²=4x的焦点为F（1，0），
设A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），D（x₄，y₄），
则k₁=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{{y}_{1}-{y}_{2}}{\frac{{{y}_{1}}^{2}-{{y}_{2}}^{2}}{4}}$=$\frac{4}{{y}_{1}+{y}_{2}}$，
同理可得k₂=$\frac{4}{{y}_{3}+{y}_{4}}$，
设AC所在的直线方程为y=m（x-2），
联立$\left\{\begin{array}{l}{y=m（x-2）}\\{{y}^{2}=4x}\end{array}\right.$，得my²-4y-8m=0，
即有y₁y₃=-8，同理可得y₂y₄=-8，
即有$\frac{{k}_{1}}{{k}_{2}}$=$\frac{{y}_{3}+{y}_{4}}{{y}_{1}+{y}_{2}}$=$\frac{\frac{-8}{{y}_{1}}+\frac{-8}{{y}_{2}}}{{y}_{1}+{y}_{2}}$=$\frac{-8}{{y}_{1}{y}_{2}}$，
设直线AB的方程为y=k₁（x-1），
联立$\left\{\begin{array}{l}{y={k}_{1}（x-1）}\\{{y}^{2}=4x}\end{array}\right.$，得k₁y²-4y-4k₁=0，
可得y₁y₂=-4，
则$\frac{{k}_{1}}{{k}_{2}}$=$\frac{-8}{{y}_{1}{y}_{2}}$=$\frac{-8}{-4}$=2．
故$\frac{{k}_{1}}{{k}_{2}}$为定值2．

点评 本题考查抛物线的方程的求法，注意运用四点共圆和正弦定理、余弦定理，考查直线的斜率的比为定值的问题，注意运用直线方程和抛物线方程联立，运用韦达定理，考查化简整理的运算能力，属于中档题．