
分析 根据一元二次不等式的解法的,对a进行讨论即可.
解答 解:由$\frac{(x+4a)(x-6a)}{2a+1}$=0得x=6a,或-4a,
(1)若2a+1>0,即a>-$\frac{1}{2}$时,不等式$\frac{(x+4a)(x-6a)}{2a+1}$>0,等价为(x+4a)(x-6a)>0,
若a=0,则不等式等价为x2>0,则不等式的解集为{x|x≠0},
若a>0,不等式$\frac{(x+4a)(x-6a)}{2a+1}$>0,等价为(x+4a)(x-6a)>0,即x>6a或x<-4a,即不等式的解集为(-∞,-4a)∪(6a,+∞),
若-$\frac{1}{2}$<a<0时,由(x+4a)(x-6a)>0,即x>-4a或x<6a,即不等式的解集为(-∞,6a)∪(-4a,+∞),
(2)若2a+1<0,即a<-$\frac{1}{2}$时,不等式$\frac{(x+4a)(x-6a)}{2a+1}$>0,等价为(x+4a)(x-6a)<0,
即6a<x<-4a,则不等式的解集为(6a,-4a),
综上所述,若a<-$\frac{1}{2}$时,不等式的解集为(6a,-4a),
若-$\frac{1}{2}$<a<0时,不等式的解集为(-∞,6a)∪(-4a,+∞),
若a=0,不等式的解集为{x|x≠0},
若a>0,不等式的解集为(-∞,-4a)∪(6a,+∞).
点评 本题主要考查不等式的解法,根据一元二次不等式的解法是解决本题的关键.注意要对a进行分类讨论.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
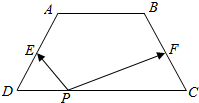 如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )
如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在等腰梯形ABCD的四条边长,有且只有8个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )| A. | (-$\frac{5}{4}$,-$\frac{9}{20}$) | B. | (-$\frac{9}{20}$,$\frac{11}{4}$) | C. | (-$\frac{9}{20}$,-$\frac{1}{4}$) | D. | (-$\frac{5}{4}$,$\frac{11}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+1 | B. | a+$\frac{3}{4}$ | C. | a2+1 | D. | $\frac{3}{4}$-a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com